En los apartados anteriores hemos visto que la comparación de dos figuras, dos tamaños o dos cantidades a y b puede formularse con el lenguaje matemático escribiendo: a / b. Definíamos a esto como razón entre dos magnitudes (ratio en latín) o comparación entre dos cantidades.
Ejemplos:
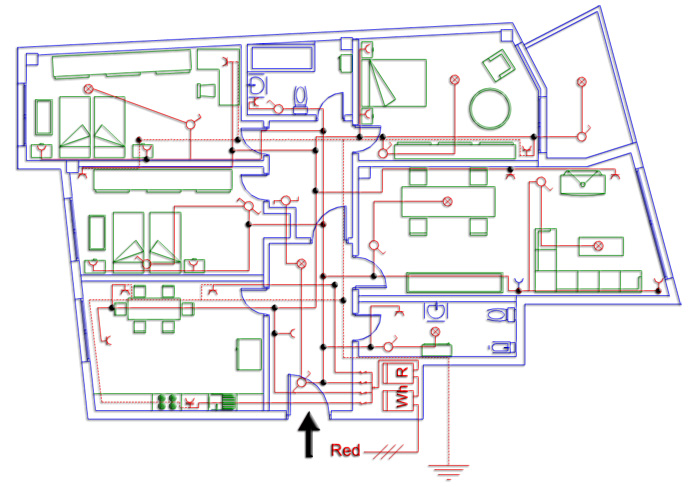
Si al comparar un dibujo con el tamaño real del objeto representado comprobamos que este último es cien veces mayor que el primero, escribiremos la razón de uno es a cien, con esta anotación: 1/100.
Si en un plano leemos, e: 1/50.000 entendemos que el tamaño de los objetos reales que allí se representan son 50.000 veces más grandes o, lo que es lo mismo, que el dibujo es 50.000 veces más pequeño.

DEFINICIÓN.

Podemos concebir la escala como la proporción o tamaño con la que se desarrolla una idea. En dibujo definimos a la escala como la proporción entre las dimensiones de un dibujo y las del objeto que representa.

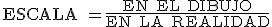
Para utilizar una escala tienes que plantearte las dimensiones del objeto a representar y llevarlo a cabo mediante un dibujo a igual, o a diferente tamaño, pero sin que éste pierda su configuración.
La escala viene representada por un quebrado, en el que el numerador expresa la magnitud del dibujo y el denominador refleja la medida real, en ambos casos la unidad en la misma: E: 1/100: una unidad del dibujo corresponde a 100 unidades en la realidad, si tomas como unidad el centímetro tienes, cada centímetro lineal en el dibujo son 100 cm en la realidad, o lo que es lo mismo un metro real.

USOS DE LA ESCALA:

• Uso Directo: Cuando pasamos de un objeto a un dibujo. Hay que multiplicar las dimensiones de la forma por la escala; ejemplo: 20 metros a E: 1/2  10 metros o 1000cm.
  
• Uso Indirecto: Pasamos de un dibujo a un objeto. Hay que multiplicar las dimensiones del dibujo por la inversa de la escala; ejemplo: 50 cm a E:1/1000   50 x 1000/1= 50.000 cm ó 500 metros.

TIPOS DE ESCALAS: natural, de ampliación y de reducción.