1.3. Teorema de Thales: la división

En los apartados anteriores hemos aprendido a dividir un segmento en dos partes iguales mediante el trazado de la mediatriz. Así pues, si dibujamos sucesivas mediatrices sobre un mismo segmento este quedará divido en el doble de divisiones: de 2 a 4, de 4 a 8 ... 2n partes iguales.
El procedimiento anterior no se puede considerar un método general ya que no permite dividir un segmento en un número cualquiera (3, 5, 6, 7...) de partes iguales.
Para resolver este problema recurriremos a la proporcionalidad directa, concepto que se desarrollará en la próxima unidad didáctica y en el que se basa el método empleado por Thales de Mileto (matemático, físico y filósofo griego) para calcular la altura de la pirámide de Keops: el teorema de Thales.
Dicho teorema dice que los segmentos resultantes de la intersección de rectas paralelas con dos rectas concurrentes r y s son directamente proporcionales.
El puente del Alamillo de Sevilla (fotografía superior), es un claro ejemplo del teorema de Thales: los cables de sujeción dividen al tablero y al mástil en partes iguales y proporcionales
El procedimiento anterior no se puede considerar un método general ya que no permite dividir un segmento en un número cualquiera (3, 5, 6, 7...) de partes iguales.
Para resolver este problema recurriremos a la proporcionalidad directa, concepto que se desarrollará en la próxima unidad didáctica y en el que se basa el método empleado por Thales de Mileto (matemático, físico y filósofo griego) para calcular la altura de la pirámide de Keops: el teorema de Thales.
Dicho teorema dice que los segmentos resultantes de la intersección de rectas paralelas con dos rectas concurrentes r y s son directamente proporcionales.
El puente del Alamillo de Sevilla (fotografía superior), es un claro ejemplo del teorema de Thales: los cables de sujeción dividen al tablero y al mástil en partes iguales y proporcionales
- Biografía de Thales de Mileto: Wikipedia.
- Cálculo de la altura de la pirámide de Keops, aplicación del teorema de Thales: caballo de letras
- Puente del Alamillo de Sevilla, estructura, materiales, imágenes, etc.. Wiki Arquitectura
División de un segmento en partes iguales.
En 7 partes iguales.
Vídeo: división de un segmento en partes iguales aplicando el teorema de Thales.
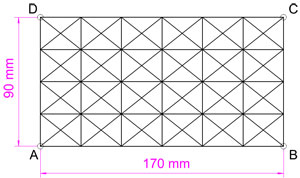 Dado el rectángulo ABCD se pide: dibujar el mosaico de 24 rectángulos empleando el teorema de Thales según el modelo dado en la imagen de la izquierda.
Dado el rectángulo ABCD se pide: dibujar el mosaico de 24 rectángulos empleando el teorema de Thales según el modelo dado en la imagen de la izquierda.
¿Necesitas ayuda para resolver este ejercicio?