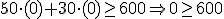Para resolver nuestro problema lo primero que haremos será representar gráficamente las restricciones en unos ejes de coordenadas:

1) Resolvemos cada inecuación por separado

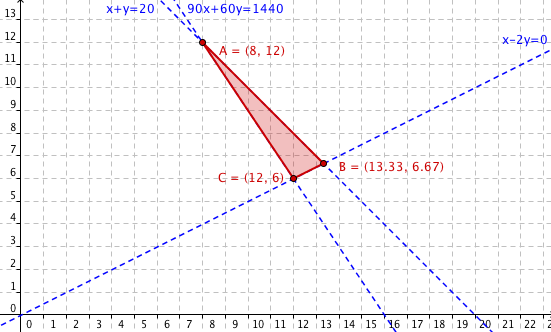
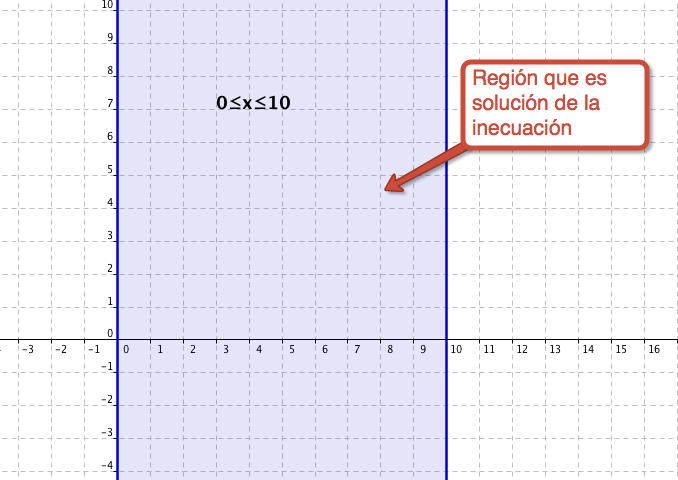
Primera restricción:0≤x≤10	Segunda restricción:0≤y≤10
Los puntos que verifican 0≤x≤10, son aquellos que están a la derecha de la recta x=0 y al mismo tiempo están a la izquierda de la recta x=10.	Los puntos que verifican 0≤y≤10, son aquellos que están por encima de la recta y=0 y al mismo tiempo están por debajo de la recta y=10.
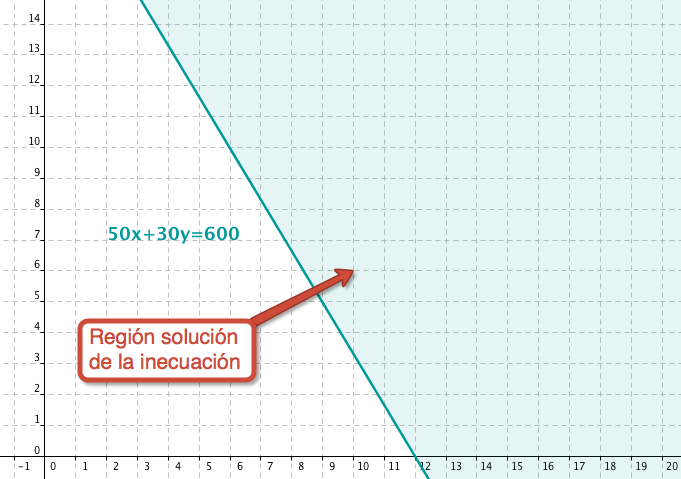
Tercera restricción: 50x+30y≥600	Con este vídeo puedes recordar como representar una recta en el plano: Recuerda que para saber el semiplano solución de una inecuación basta con sustituir un punto, el (0,0) por ejemplo si no pertenece a la recta. Si el punto verifica la inecuación, el semiplano que contiene el punto es la solución, en caso contrario es el otro semiplano.
En este caso lo primero que hacemos es representar la recta 50x+30y=600. Una vez representada basta sustituir un punto, el (0,0) por ejemplo, para saber cual es el semiplano solución. Si sustituimos (0,0) en 50x+30y≥600 obtenemos: Que es falso, por lo tanto, el semiplano solución es el que no contiene al origen de coordenadas.

 

2) Calculamos la intersección o región común de las soluciones de todas las inecuaciones

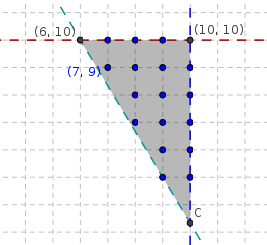
Representamos las tres regiones en la misma gráfica, la región intersección será el lugar donde se encuentre la solución que buscamos. Marca la casilla correspondiente para ver su solución.

La solución a nuestro problema debe estar en la región determinada por las distintas desigualdades. Esta región recibe el nombre de región factible.

En nuestro caso la región factible está acotada, es decir, es un polígono. Hay problemas donde la región no está acotada. En cualquier caso siempre es un polígono o una región convexa.

Nos falta añadir una condición. No podemos enviar 6,5 furgonetas, por lo tanto, el número de furgonetas de cada tipo han de ser números enteros. Por lo tanto, la solución la buscaremos entre los puntos que están dentro de la región factible y sus coordenadas son números enteros.En nuestro caso hay 20 posibles soluciones.

Habrá que averiguar en cuál de ellos la función F(x,y)=120x+60y toma un valor menor. Por ejemplo para el punto (7,9), que nos indica 7 furgonetas del tipo I y 9 furgonetas del tipo II, le corresponde un gasto de F(7,9)=120·(7)+60·(9)=840+540=1380 €.

¿Podemos mejorarlo?

Imagínate que en vez de 20 posibles soluciones hubiera 15000. Vamos a buscar un método en el que podamos resolver el problema sin necesidad de ir calculando punto a punto hasta ver cuál es el coste mínimo.