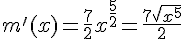2.2. Así voy a la deriva
Si tenemos una función  denominamos función derivada de
denominamos función derivada de  respecto a la variable
respecto a la variable 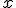 a una nueva función que para cada valor
a una nueva función que para cada valor 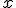 nos proporciona la derivada de la función en el punto
nos proporciona la derivada de la función en el punto 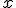 . A la función derivada de
. A la función derivada de  la denotaremos
la denotaremos 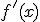 , aunque también la puedes ver representada como
, aunque también la puedes ver representada como 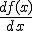 . De esta forma tenemos que:
. De esta forma tenemos que:
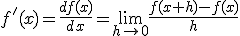
Recuerda que con esta definición, la función derivada nos proporciona, para cada punto 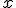 , la pendiente de la recta tangente a la función en en punto
, la pendiente de la recta tangente a la función en en punto 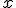 .
.
 |
| Carretera. Imagen obtenida del banco de imágenes del ITE |
En la construcción de una carretera, uno de los puntos con los que hay que tener especial cuidado es en las curvas. Dependiendo de lo cerrada que sea la curva, debe tener más peralte o menos para evitar que los coches se salgan de la misma. En la construcción de una carretera, una de las curvas se adapta perfectamente a la función 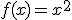 . Los técnicos desean tener una función que les proporcione en cada uno de los puntos de la curva la pendiente que tendrá la recta tangente a la misma. ¿Puedes ayudarles?
. Los técnicos desean tener una función que les proporcione en cada uno de los puntos de la curva la pendiente que tendrá la recta tangente a la misma. ¿Puedes ayudarles?
Aquí te ofrecemos información sobre la derivada de algunas funciones. Pulsando sobre el nombre de cada una de ellas te mostraremos la derivada resultante y la gráfica en la que puedes comprobar que la función derivada es aquella que de cada punto nos proporciona la pendiente de la recta tangente a la función en ese punto.
 |
Derivada de una constante f(x) = k |  |
Derivada del logaritmo neperiano f(x) = L(x) | |
 |
Derivada de la identidad f(x) = x |  |
Derivada de la exponencial natural f(x) = ex | |
 |
Derivada de la proporcionalidad inversa f(x) = 1/x |  |
Derivada del seno f(x) = sen(x) | |
 |
Derivada
de la raíz cuadrada f(x) =
|
 |
Derivada del coseno f(x) = cos(x) | |
 |
Derivada de la potencia f(x) = xn |  |
Derivada de la tangente f(x) = tg(x) | |
 |
Otras derivadas |
 |
En la imagen de la derecha te ofrecemos un listado en el que aparece una función y al lado aparece su función derivada. Este mismo listado te lo ofrecemos en el siguiente documento. Como has podido observar, todos los resultados que aparecen en esta tabla son fruto de aplicar la definición de derivada de una función. Es conveniente aprenderse esta tabla para no tener que recurrir una y otra vez a la definición cada vez que necesitemos derivar una función.
Calcula la derivada de las siguientes funciones:
a) 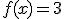 |
b) 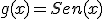 |
c) 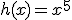 |
d) 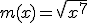 |
Aquí te dejamos un vídeo de interés para que profundices en la aplicación de la derivada en el mundo que te rodea:
|
|
| En esta programa pueden observar la gráfica, sus derivada y la fórmula de su derivada.
Todos los applets trabajan con expresiones tales como "x+3" o "sqrt(k*t)". Estas expresiones pueden usar los operadores +, -, *, /, ^, y ** (donde ambos ^ y ** indican exponenciación), y en estos pueden ser usados las constantes matemáticas pi
y e. También se utilizan varias funciones Matemáticas: sin, cos, tan, sec,cot, csc, arcsin, arccos, arctan, exp, ln, log2, log10, abs, sqrt, trunc, round, floor, ceiling, y cubert. (Aqui, "abs" es el valor absoluto de la función y "cubert" es la raíz cúbica de la función.)
|
|
Calculadora de derivadas obtenida de Universidad de Puerto Rico en Aguadilla |
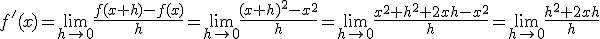
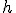 quedando:
quedando:
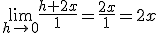
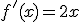
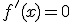
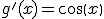
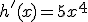
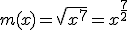 y por tanto
y por tanto