2.1. Tocando la gráfica
Idea gráfica de derivada a una función en un puntoMueve los puntos A y B y observa
Mariano Real Pérez, Creación realizada con GeoGebra |
Observa que la pendiente de la recta que pasa por 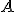 y por
y por 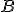 es:
es: 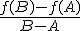
que lo hemos indicado en la imagen como pendiente de la recta secante que pasa por 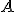 y por
y por 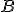 .
.
A medida que en la imagen aproximamos el punto 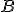 al punto
al punto 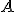 la recta secante que pasa por
la recta secante que pasa por 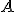 y
y 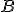 se va acercando a la recta tangente a la función
se va acercando a la recta tangente a la función  en el punto
en el punto 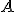 , por lo que la expresión
, por lo que la expresión 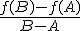
se va acercando a la pendiente de la recta tangente a la función  en el punto
en el punto 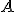 . De esta forma tenemos que:
. De esta forma tenemos que: 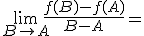 Pendiente de la recta tangente a la función
Pendiente de la recta tangente a la función  en el punto
en el punto 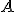 .
.
Generalizando lo anterior tenemos que:
Si tenemos una función  , la derivada de la función en x=a,
, la derivada de la función en x=a, 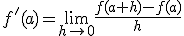
es la pendiente de la recta tangente a  en el punto de abcisa
en el punto de abcisa 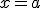 .
.
De esta forma, si tenemos una función  , su función derivada
, su función derivada 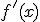 es la función que en cada punto toma el valor de la pendiente de la recta tangente a
es la función que en cada punto toma el valor de la pendiente de la recta tangente a  en ese punto.
en ese punto.
El siguiente vídeo te explica gráficamente este hecho:
Por tanto, la recta tangente a la función en el punto  es:
es: 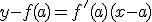 .
.
A la recta perpendicular a esta recta tangente en el punto  se le llama recta normal. Así, la ecuación de la recta normal es:
se le llama recta normal. Así, la ecuación de la recta normal es: 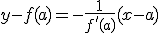 .
.
Hemos aplicado que la pendiente de una recta, m, y la de una recta perpendicular a ella, m', verifican que m·m'=-1.
En la siguiente ventana interactiva puedes observar para distintas funciones en un punto concreto la recta tangente (en verde) y la recta normal (en violeta).
|
Applet obtenida de los recursos didácticos de Descartes. |
Derivada de la función senoMueve el punto A a lo largo de la gráfica
Mariano Real Pérez, Creación realizada con GeoGebra |
El valor numérico de la pendiente de la recta tangente a la función de la gráfica anterior es en los puntos máximos.
El valor numérico de la pendiente de la recta tangente a la función de la gráfica anterior es en los puntos mínimos.
La función que resulta como función derivada es la función .
La pendiente de la recta tangente a la función en el punto 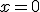 es
.
es
.
La pendiente de la recta normal a la función en el punto 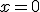 es
.
es
.
Te proponemos ahora un ejercicio que ya has realizado en el apartado 1.3. de forma que observes qué pasa gráficamente.
Si tenemos la función 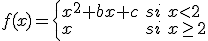
Calcula los calores de 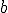 y de
y de  para que la función sea derivable en
para que la función sea derivable en 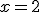 . Observa en la gráfica que aparece más abajo lo que sucede con esos valores.
. Observa en la gráfica que aparece más abajo lo que sucede con esos valores.
|
Applet obtenida de la web de Educastur |
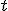 para que la recta
para que la recta 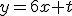 sea tangente a la función
sea tangente a la función 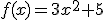 .
.
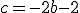 .
. 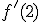 los límites laterales deben coincidir, llegamos a que
los límites laterales deben coincidir, llegamos a que 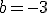 .
. 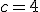 .
.
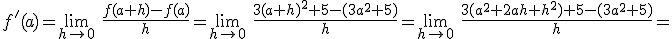
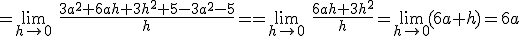 .
.
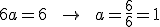 .
.
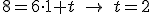 .
.