1.2. Entre planos
 |
| Imagen tomada del Banco de Imágenes y Sonidos del I.T.E. |
Si te fijas a tu alrededor, ¿que ves? Seguro que Geometría por todos lados. Ya hemos comentado a lo largo del curso que las matemáticas forman parte del entorno cotidiano . Salvo que vivas en lo más recóndito del monte o campo seguro que a tu alrededor tienes construcciones creadas por la mano del hombre y en ellas encuentras multitud de elementos geométricos. En concreto, seguro que puedes encontrar multitud de planos en todas las posiciones imaginables.
Lo que vamos a hacer en este apartado es aprender a medir las distancias a planos suponiendo que nos encontramos en un sistema de referencia tridimensional.
La distancia de un punto a un plano se define como la medida entre el punto y el pie de la perpendicular sobre el plano lanzada desde el punto.
Para calcularla, la mejor manera es hallar la recta que pasa por el punto y es perpendicular al plano y por tanto su vector dirección es el vector normal del plano. Al determinar el punto de corte de esa segunda recta y el plano obtenemos el punto que es pie de la perpendicular y basta calcular la distancia entre los dos puntos.
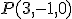 y el plano
y el plano 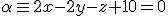 .
.
 |
Nos hemos colocado en la plaza de Santa Teresa, junto a una estatua, frente a las murallas de Ávila y queremos saber la distancia que hay hasta la puerta de entrada al recinto fortificado.
A través de una foto de satélite de Google Maps nos hemos situado en el punto 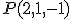 y las murallas las hacemos coincidir con el plano 2x-10y+11z-208=0.
y las murallas las hacemos coincidir con el plano 2x-10y+11z-208=0.
Halla la distancia que separa ambos lugares.
Igual que ocurría en el apartado anterior, aquí también hay distintas maneras de hallar la distancia de un punto a un plano. Veamos algunas otras.
- Si escribimos la ecuación del plano en para métricas y elegimos un punto genérico del plano (que dependerá de dos parámetros) basta imponer que el vector que une el punto exterior y ese punto genérico sea perpendicular al plano, por lo que debe ser o proporcional al vector normal o perpendicular a los dos vectores de dirección. El inconveniente de este método es que nos aparece un sistema de dos ecuaciones con dos incógnitas.
- Si tomamos un punto cualquiera del plano y los dos vectores de dirección, con estos dos últimos y el vector que une el punto exterior y el punto elegido podemos construir un paralelepípedo cuyo volumen es fácil de calcular según vimos en el tema anterior. Como conocemos el área de la base (que sería el módulo del producto vectorial de los vectores dirección) basta hallar la altura del prisma que es la distancia del punto al plano. Ese es el método que se utiliza en el siguiente applet de Descartes, en el que puedes escribir las coordenadas del punto y los datos del plano (punto y vectores dirección). Aumentando el pulsador Paso puedes ver como se resuelve el problema.
Applet de Descartes creado por Juan Simón Santamaría bajo licencia Creative Commons.
Por último para hallar la distancia entre dos planos tenemos las siguientes posibilidades, según su posición relativa.
- Si los dos planos se cortan o son coincidentes, la distancia entre ellos es cero.
- Si los dos planos son paralelos, basta elegir un punto P cualquiera de uno de los planos y hallar la distancia de P al otro plano.
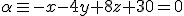 y
y 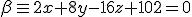 .
.
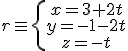 .
.
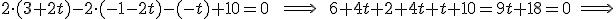
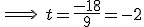 y sustituyendo en la recta obtenemos el punto
y sustituyendo en la recta obtenemos el punto 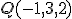 .
.
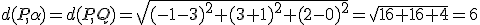 .
.