3.1. La derivada. Interpretación

Actividad

Se define Tasa de variación instantánea en el punto x=a (TVI_a) como:

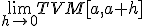
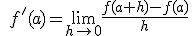
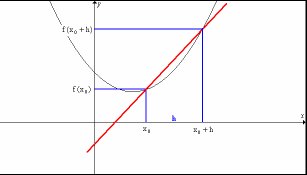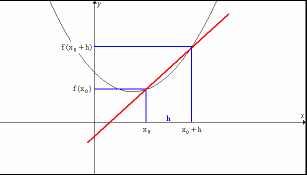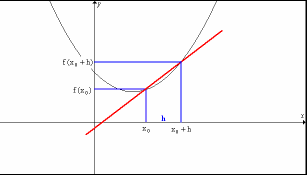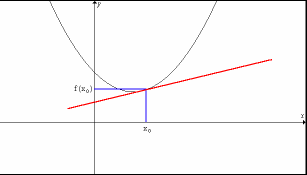En realidad y para simplificar a TVI_a se le llama derivada de la función f(x) en el punto x=a y se denota por f´(a). La expresión mas conocida es:

En los dos dibujos se muestra las interpretaciones geométricas de la TVM en el primero y de la derivada en el segundo.

Si la TVM era la pendiente de la recta secante (que pasa por los dos puntos (a, f(a)) y (a+h, f(a+h))) al hacer h tender a 0, los puntos tienden a coincidir. La recta que era secante a la función en los puntos, es ahora tangente a la función en un punto. Por tanto:

Actividad

La derivada de una función en un punto es la pendiente de la recta tangente a la función en ese punto.

Ejemplo o ejercicio resuelto

Calculemos de forma intuitiva la derivada de la función y=x² en el punto a=1. Para ello vamos a utilizar la definicion de TVM Construimos la siguiente tabla:

Intervalo [a,a+h]	[1;1,1]	[1;1,01]	[1;1,001]	[1;1,0001]	[1;1,00001]	......	[1,1]
TVM	2,1	2,01	2,001	2,0001	2,00001	....	2

Intervalo [a,a+h]	[0,99;1]	[0,999;1]	[0,9999;1]	[0,99999;1]	.......	[1,1]
TVM	1,9	1,99	1,999	1,9999	....	2

En la primera tabla nos acercamos al punto por la derecha y el resultado es 2.

En la segunda nos acercamos al punto por valores menores (izquierda) y el resultado el 2. Por tanto, decimos que la derivada de la función y = x², en x=1 es 2, o escrito de forma más elegante, f '(1) = 2.

Objetivos

Para que exista la derivada de una función en un punto deben de existir la derivada lateral a la izquierda y a la derecha y coincidir.

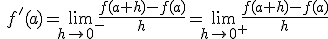
Si quieres saber más de las derivadas pincha aquí.

AV - Pregunta Verdadero-Falso

Responde verdad o falso

1) La derivada es el límite de la Tasa de variación.

Verdadero Falso

2) La gráfica de las subidas y bajadas de la bolsa es continua.

Verdadero Falso

3) La función recorrido de un ciclista en una etapa en función del tiempo es discontinua.

Verdadero Falso

4) Una función derivable en un punto es continua en ese punto.

Verdadero Falso

Para saber más

En el siguientes vídeos de la serie Universo Mecánico puedes ver los aspectos históricos que llevaron a la creación de la derivada y algunas de sus aplicaciones en la vida cotidiana. Aparecen también las reglas sobre como calcular derivadas de distintas funciones, algo que veremos el próximo curso.

« Anterior