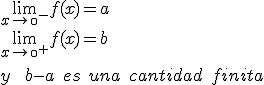2.1. Un salto finito
Una función se dice que es continua cuando la gráfica se puede trazar sin levantar el lápiz. Este concepto nos es fácil explicarlo por el conocimiento de línea continua y discontinua en nuestras carreteras
 |
 |
|
8. Continua: Imagen en ojodigital.com |
9. Discontinua: Imagen en amapolas.cpjv.net bajo licencia de Creative Commons |
En una función pasa algo similar observa esta función:
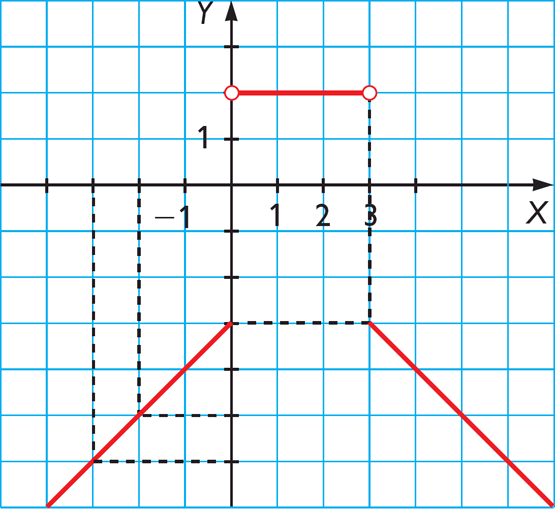 |
Si damos valores (nos acercamos) al cero por la izquierda (valores menores pero muy próximos al cero) la función se acerca al valor -3. Si por el contrario nos acercamos por valores mayores al cero (siempre muy próximos) la función se acerca al valor 2.
Este es un caso de salto, discontinuidad de salto finito. De la misma forma podemos ver que existe un salto finito en x=3.
En Matemáticas este procedimiento de acercarse por valores menores o mayores se llama límite y se denota
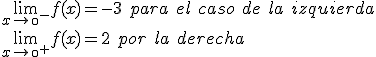
Una función tiene una discontinuidad de salto finito en un punto si la diferencia entre los límites laterales es finita.