2.- El binomio perfecto.
|
|
5. Jacob Bernouilli:Imagen en Wikimedia Commons bajo licencia Creative Commons. |
Hay variables que se presentan con frecuencia en nuestro alrededor. Una de ellas es la variable binomial. Esta variable fue enunciada por Jacob Bernoulli hacia el año 1700.
Veamos algunos ejemplos de este tipo de variable:
- Número de chicos en una familia con "n" hijos
- Número de clientes que anulan la reserva de un hotel, vuelo, restaurante, etc. con "n" habitaciones, asientos, mesas, etc.
- Número de piezas defectuosas en un lote de "n" piezas.
- Número de preguntas falladas en un test con "n" preguntas.
Binomial
Una variable aleatoria sigue una binomial si:
1º) Hay un experimento aleatorio que se repite n veces con independencia (Tener n=6 hijos, el sexo de cada uno es independiente del anterior, contestar un test de n=30 preguntas el acierto o no, no depende de la cuestión anterior)
2º) En cada prueba solo puede darse dos situaciones: éxito o fracaso (ser varón o no, acertar o no). Las probabilidades de ambos suman uno pero no tienen que ser la misma.
p= probabilidad de obtener éxito
1-p= probabilidad de no obtener éxito (fracaso)
3º) La variable se define como el número de éxitos conseguidos: X = número de éxitos conseguidos en los n experimentos.
Para simplificar, en adelante esta variable aleatoria se le designará por B(n,p)
 |
El 10% de los turismos que se vendieron en el 2009 fueron destinados a taxis (según fuentes de una revista nacional de motor). En un día la marca de automóviles TOMOYA de cierta ciudad vendió 3 turismos. Vamos a describir la variable aleatoria X=n.º de turismos destinados a taxis de la marca TOMOYA. Designemos por T (taxi) y F si es para uso particular.
Las probabilidades de que al elegir un coche al azar, éste sea dedicado a taxi o a uso particular serán 0,1 y 0,9 respectivamente:
p(T)=0,1 y p(F)=0,9
Es decir, la variable X se trata de una B(3; 0,1). En la tabla siguiente desarrollamos las probabilidades de X.
| Resultados | Probabilidad | nº de éxitos (X) |
| FFF | (0,9)(0,9)(0,9)=0,729 | X=0 |
| FFT | (0,9)(0,9)(0,1)=0,081 | X=1 |
| FTF | (0,9)(0,1)(0,9)=0,081 | X=1 |
| TFF | (0,1)(0,9)(0,9)=0,081 | X=1 |
| FTT | (0,9)(0,1)(0,1)=0,009 | X=2 |
| TFT | (0,1)(0,9)(0,1)=0,009 | X=2 |
| TTF | (0,1)(0,1)(0,9)=0,009 | X=2 |
| TTT | (0,1)(0,1)(0,1)=0,001 | X=3 |
Agrupando los datos por los valores de X la distribución de probabilidad quedaría:
| X | 0 |
1 |
2 |
3 |
| pi | 0,729 | 0,243 | 0,027 | 0,001 |
Si obsevamos con atención los resultados podemos expresar estos como sigue:
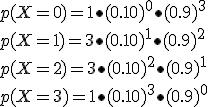
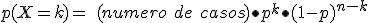
El número de casos que se pueden dar con k éxitos en n experimentos se designa por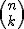 
y en el siguiente apartado veremos cómo se calcula.
Función de probabilidad de una Binomial
Curiosidad
 |
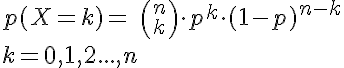
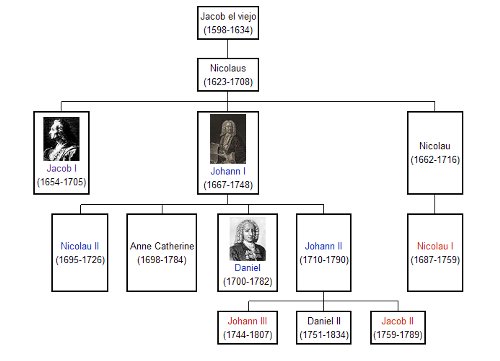Los Bernoulli (o Bernouilli) son una familia de matemáticos y físicos suizos procedentes de la ciudad de Basilea, que irrumpió en el mundo científico a finales del siglo XVII.
El fundador de esta familia fue Jacob el viejo, nacido en Amberes (Bélgica), un hugonote que se trasladó a Basilea en 1622 por motivos de persecución religiosa. Se casó tres veces y sólo tuvo un hijo, Nikolaus. Éste se casó y tuvo una docena, de los cuales cuatro llegaron a edad adulta; dos de ellos se convirtieron en matemáticos de primer orden: Jakob, nacido en 1654, y Johann, nacido en 1667. Ambos estudiaron la teoría del cálculo infinitesimal de Leibniz y desarrollaron aplicaciones de la misma.
Jakob Bernoulli (Basilea, 27 de diciembre de 1654 - 16 de agosto de 1705), también conocido como Jacob, Jacques o James Bernoulli, fue un matemático y científico. Siendo joven, su padre lo envió a la Universidad de Basilea para estudiar filosofía y teología, con el ánimo de que se convirtiera en teólogo. Pero Jakob continuó, a escondidas, las que eran sus auténticas aficiones la física y las matemáticas, según confiesa en su diario.
Su obra maestra fue Ars Conjectandi (el Arte de la conjetura), un trabajo pionero en la teoría de la probabilidad. La publicó su sobrino Nicholas en 1713, ocho años tras su muerte. Los términos ensayo de Bernoulli y números de Bernoulli son resultado de su trabajo. También existe un cráter en la Luna bautizado cráter Bernoulli en honor suyo y de su hermano Johann.
Para saber más