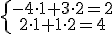2.2. ¿Cuántas soluciones podemos encontrar?
Poco a poco vamos obteniendo información sobre el interesante mundo de las ecuaciones. El camino que nos interesa recorrer es descubrir cómo solucionarlas para resolver los problemas cotidianos en los que nos puedan aparecer estos elementos.
Ya vimos que si tenemos una ecuación con una incógnita puede tener una o unas pocas soluciones, si la ecuación tiene dos incógnitas, entonces tiene infinitas soluciones. ¿Y con los sistemas qué pasa? Puedes pensar, por lo visto en el apartado anterior, que siempre tiene una solución única, eso sí formada por dos valores. Pero eso no siempre es así.
 |
Te ponemos un ejemplo muy simple. Si he comprado un cuaderno y un rotulador y me han costado 4,25 €, hay muchos precios distintos para el cuaderno y para el rotulador. Si ahora me dicen que dos cuadernos y dos rotuladores iguales cuestan 8,50 €, es verdad que tengo otra ecuación, pero realmente no me aporta ninguna información nueva, pues ese dato podía haberlo deducido directamente de la anterior, por lo que sigo sin saber cuánto vale exactamente el cuaderno o el rotulador.
Para ver la cantidad de soluciones de un sistema vamos a aprovechar las posibilidades gráficas y a trabajar con un applet de Geogebra como el que trabajaste en el punto 1. Ahora vamos a tener dos ecuaciones, una de coeficientes a, b y c y la otra de coeficientes p, q y r.
Desde el punto de vista gráfico, ya dijimos que todos los puntos de la recta de ecuación a·x+b·y = c son solución de esa ecuación.
Lógicamente en un sistema de dos ecuaciones, la solución será un punto que pertenezca a la vez a la recta correspondiente a la primera ecuación y a la recta de la segunda, es decir, un punto común a las dos rectas. Puedes verlo en la ventana anterior. Ese punto será el de corte de ambas rectas.
En general tendremos los siguientes casos:
a) Las dos rectas tienen un sólo punto común, entonces el sistema se llama Compatible Determinado.
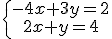 tiene como solución el par de valores x=1, y=2.
tiene como solución el par de valores x=1, y=2.
b) Las dos ecuaciones son paralela paralelas y entonces no tienen ningún punto común. En este caso el sistema se llama Incompatible.
Utiliza el applet de Geogebra y comprueba que en el sistema de ecuaciones 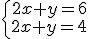 las dos rectas son paralelas y por lo tanto no hay punto de corte. Para ello da los valores a=2, b=1 y c=6 para la primera ecuación y p=2, q=1 y r=4 para representar la segunda ecuación.
las dos rectas son paralelas y por lo tanto no hay punto de corte. Para ello da los valores a=2, b=1 y c=6 para la primera ecuación y p=2, q=1 y r=4 para representar la segunda ecuación.
c) Si las dos ecuaciones son la misma o proporcionales (recuerda el ejemplo del cuaderno y el rotulador) entonces las rectas coinciden y todos los puntos de una de las ecuaciones también pertenecen o satisfacen a la otra ecuación. En este caso hay infinitas soluciones y el sistema se llama Compatible Indeterminado.
Compruébalo en la ventana de Geogebra dibujando el sistema 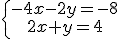 .
.
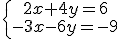 . Responde a las siguientes cuestiones.
. Responde a las siguientes cuestiones.
|
Para Practicar
Puedes practicar los conceptos aprendidos realizando los dos primeros test de la parte de Clasificación de la página de Álgebra con papas.
|