Tal y como hemos explicado anteriormente, cualquier sistema de regulación y control puede representarse por medio de un diagrama de bloques. En él se reproducirá la forma en la que están relacionadas las salidas en función de las entradas de todos los elementos que constituyen el sistema.

De cara a facilitar la comprensión de los procesos de control, es muy conveniente realizar la simplificación y reducción de estos diagramas.

En este apartado estudiaremos una serie de pautas de actuación para operar con estos diagramas de bloques y conseguir simplificarlos y reducirlos a otros equivalentes más operativos y más sencillos de manejar.

Comparadores o detectores de error

Son sumadores, se representan como se indica en la figura, realizan la función de efectuar sumas algebraicas, respetando el signo de las variables que entran en ellos.

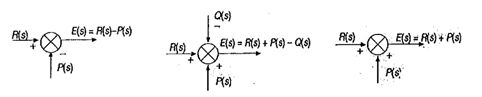Imagen 15. Recurso propio.

Combinación entre líneas de actuación

La interacción entre los distintos tipos de bloques se representa mediante líneas de actuación en las que las flechas indican el sentido del flujo de información.

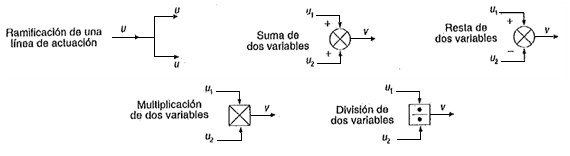Imagen 16. Recurso propio.

Partiendo de estos conceptos básicos es posible realizar las siguientes combinaciones básicas de bloques:

• Conexión serie

En este tipo de conexión la salida de un bloque constituye la entrada del siguiente:

Imagen 17. Recurso propio.

• Conexión paralelo

Según se representa en la figura, en este caso se debe disponer de un sumador en la salida:

Imagen 18. Recurso propio.

• Conexión en anillo con realimentación directa:

Corresponde a un diagrama como el representado en la figura.

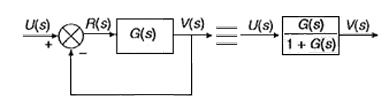Imagen 19. Recurso propio.

En el comparador tenemos:

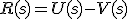
Por otro lado en el bloque;

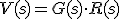
Sutituyendo R(s) queda:

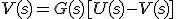
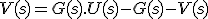
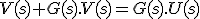
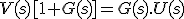
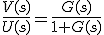
• Conexión en anillo con realimentación a través de un segundo elemento:

Cuando en el bucle de realimentación existe un bloque, como el representado en la figura. El controlador derivativo se opone a desviaciones de la señal de entrada, con una respuesta que es proporcional a la rapidez con que se producen éstas.

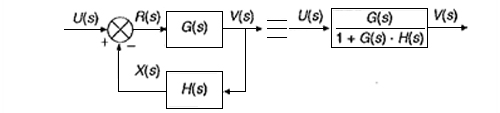Imagen 20. Recurso propio.

Donde las funciones de cada elemento son:

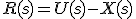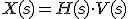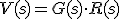Primero sustituimos en R(s):

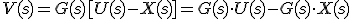
Luego cambiamos X(s) por su valor y nos queda:

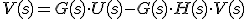
Agrupando y despejando obtenemos la función de transferencia:

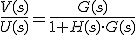
• Transposición de ramificaciones y nudos:

Se recurre a estas técnicas de transposición para facilitan la reducción y simplificación de diagramas de bloques. A continuación se muestran los casos más importantes:

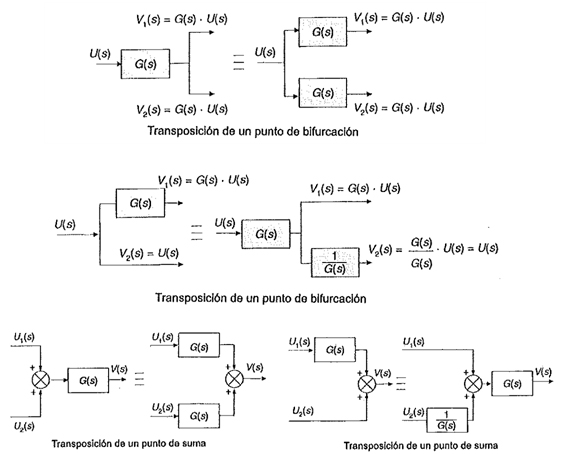Imagen 21. Recurso propio.