3. Códigos binarios
Un sistema binario es cualquier sistema de representación de información mediante variables binarias. Se basa en representar en formato binario la información numérica decimal.
Representamos en el siguiente diagrama algunos de los códigos binarios más importantes.
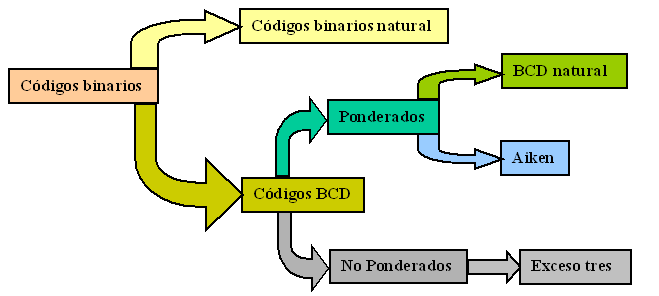 |
| Imagen 06. Rafael Domínguez. Creative Commons |
Vamos a describir los códigos más importantes anteriores y algunos otros de usos más puntuales:
Código binario natural.
Consiste en representar directamente el número decimal en binario, o lo que es lo mismo cada número decimal tiene su correspondiente en binario. Ejemplo 35(10 = 100011(2
Códigos BCD (Decimal codificado en binario).
Con estos códigos, para representar un número decimal en binario, se transforman cada una de las cifras que constituyen el número decimal separadamente, en el caso anterior el número 35, transformado en binario sería el resultado de transformar primero 3, y después 5.
Código BCD natural (8-4-2-1).
Se basa en representar cada dígito decimal a su correspondiente binario natural. Cada dígito corresponde a un grupo de 4 bits.
El código BCD es un código ponderado; a cada bit le corresponde un valor (peso) de acuerdo con la posición que ocupa, igual que el binario natural. Los pesos son: 8-4-2-1. La representación del 1 al 9 corresponde con el binario natural, pero a partir del número decimal 10, se precisan grupos de 4 bits por dígito. Para codificar un número decimal de N dígitos se requieren N grupos de 4 bits.
Ejemplo 35 = 0011 0111. Es decir 3 (0011) y 5 (0101)
Ejemplo 13 = 0001 0011
Ejemplo 2001 = 0010 0000 0000 0001 (2 = 0010; 0 = 0000; 0 = 0000;1 = 0001)
Código Aiken (2-4-2-1).
También es un código ponderado, aunque ahora los pesos de las cifras según su posición serán: 2, 4, 2 y 1.
Ejemplo 35 = 0011 1011. Es decir 3 (0011, si miramos el peso de los dígitos será = 0 + 0 + 2 +1 = 3) y 5 (1011, si miramos el peso = 2 + 0 +2 +1).
Código exceso tres.
Es un codigo BCD no ponderado, cada combinación se obtiene sumando el valor 3 a cada combinación binaria BCD natural (8-4-2-1).
Ejemplo 35 = 0110 1000, es decir:
3 = 3 + 3 = 6 = (0110)BCDnatural y
5 = 5 + 3 = 8 = (1000)BCDnatural.
Código exceso tres paridad impar.
En ocasiones se utilizan códigos que son especialmente útiles para algún cometido concreto, esto sucede con el código que vamos a analizar, se emplea para detectar si ha habido algún error en la transmisión de los datos codificados, de modo que emplea cinco dígitos en lugar de cuatro, pero de ellos el primero es un bit de paridad, para obligar a que cada grupo de cinco bits tenga un número impar de unos; si esto es así, es porque el dato transmitido es correcto, y entonces se procesa la información transmitida que es la que resulta de decodificar los cuatro últimos bits. Ejemplo 35 =1 0110 0 1000. Es decir 3 (1 0110) y 5 (0 1000).
La siguiente tabla muestra la equivalencia entre los distintos códigos binarios analizados.
 |
| Imagen 07. Recurso propio. |
OTROS CÓDIGOS
Código dos entre cinco.
En los años 40 se utilizó un código más sofisticado llamado dos-entre-cinco, que se basa en que cada conjunto de cinco bits (llamado penta-bit) debe tener únicamente dos unos, uno entre los dos primeros bits y otro en los tres últimos, de forma que se podría detectar posibles errores cuando cada pentabit no cumple esta condición.
También existen otros códigos que no solo son capaces de detectar errores, sino que también son capaces de corregirlos, como es el código de Hamming, formados por siete bits y que es probablemente el más empleado de este tipo.
Otro tipo de códigos son los que tienen la característica de que entre una combinación y la siguiente solamente difieren en un bit, a los códigos que tienen esta característica se les llama progresivos, como es el caso del código Gray.
Se llaman códigos reflejados, aquellos que tienen la característica de la combinación de dos números decimales que sumen nueve, se escriben igual sin más que cambiar 1 por 0 y 0 por 1. Esta característica la tienen los códigos Aiken y exceso tres, como puedes comprobar observando la tabla anterior.
También existen códigos capaces de transmitir información no solo numérica, sino letras, símbolos, operaciones,... de ellos el más común es el código ASCII (American Standard Code for Information Interchange), que es el empleado por casi todos los sistemas informáticos. Se creó en 1963 por ASA (Comité Estadounidense de Estándares) para reordenar y expandir los caracteres y símbolos empleados en telegrafía por la compañía Bell, en la actualidad tiene 5852 combinaciones diferentes.
Cada vez que tecleas en tu ordenador, sin saberlo estás empleando el código ASCII.
Si en alguna ocasión tienes que utilizar un carácter que no esté incluido en un teclado, por ejemplo si tuvieses que escribir la letra Ñ en un teclado que no disponga de ella, debes mantener presionada la tecla “Alt” y sin dejar de presionarla pulsar el número “165” en el teclado numérico, esa es la combinación correspondiente a la letra ñ mayúscula en el código ASCII. Puedes consultar la wikipedia para profundizar sobre este código
|
|
|