1. Regla de las fases
 La primera cosa que deberá conocer serán los grados de libertad del sistema, es decir, cúantas variables se pueden modificar en él sin que cambie su estructura.
La primera cosa que deberá conocer serán los grados de libertad del sistema, es decir, cúantas variables se pueden modificar en él sin que cambie su estructura.
Regla de las fases de Gibbs
El número de variables (temperatura, presión, concentración, ...) , que en un sistema material podemos modificar libremente se llama GRADOS DE LIBERTAD.
La regla de las fases de Gibbs define la siguiente ecuación, que permite calcular las fases, grados libertad o componentes de un sistema, para que coexista equilibrio en nuestro sistema material.
|
F+P=C+2 |
F = número de grados de libertad
P = número de fases presentes.
C = número de componentes (A/B, etc.)
2 = es el número de variables de estado del sistema (temperatura y presión).
En los casos que nosotros trataremos, el efecto de la variación de la presión es despreciable, así establecemos que: p=1 atm=constante durante todo el proceso.
Así pues, la regla de las fases queda establecida para nuestros propósitos como:
| F+P=C+1 |
Veamos con un ejemplo la utilidad de esta ecuación, sobre un diagrama de equilibrio binario de una aleación de dos componentes cualquiera A y B.
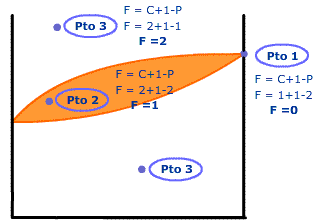 |
| Imagen 05. Elaboración propia. |
Punto 1. Estamos en la situación en que, si nos fijamos en la concentación de los componentes, nos encontramos un metal puro, y si nos fijamos en la temperatura, nos situamos en su punto de fusión ya que todo el líquido se convierte en sólido.
Por tanto:
- los componentes son 1 (100%A + 0% B, es decir metal puro A): C=1
- las fases son 2 (sólido + líquido, pues al estar en el punto de fusión ya se están empezando a formar los primeros cristales de sólido): P=2
Así pues, aplicando la regla de las fases de Gibbs obtenemos que F=0, con lo que podemos deducir que el punto de fusión es un punto fijo que se da a una temperatura y presión fijas, ya que no hay ningún grado de libertad.
Punto 2. Si nos situamos en un punto donde coexisten dos fases:
- los componentes son 2 (los dos metales de la aleación): C=2
- las fases son 2 (sólido + líquido): P=2
En esta situación obtenemos que F=1. Es decir, tenemos un único grado de libertad, con lo que es posible mantener la microestructura de dos fases mientras se modifica la temperatura del material (en un rango limitado).
Punto 3. Cuando nos situamos en la región donde hay una sola fase a una composición intermedia:
- los componentes son 2 (los dos metales de la aleación): C=2
- las fases son 1 (sólido o líquido): P=1
Es por esto que F=2, por lo que tenemos dos grados de libertad, es decir, podemos variar tanto la temperatura como la composición de la aleación en un rango limitado manteniendo la microestructura de la fase.
Ejemplo
Cálculo de F, el número de grados de libertad con la regla de fases de Gibbs, en tres puntos distintos del diagrama de fases del agua pura:
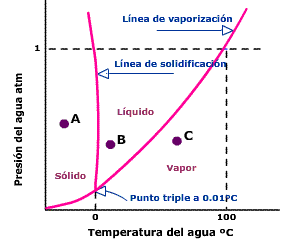 |
| Imagen 06. Elaboración propia. |