1.3. And the winner is...
 |
| Imagen de House Of Sims bajo licencia Creative Commons. |
Bien, pues ya sólo nos queda comprobar que efectivamente, ese candidato a solución, lo es. Para ello tenemos que utilizar nuevamente lo que hemos visto en el tema 2 de la unidad:
- Si en x=a, f '(a) = 0 y f ''(a) > 0, el punto x=a es un mínimo relativo.
- Si en x=a, f '(a) = 0 y f ''(a) < 0, el punto x=a es un máximo relativo.
Por tanto, habrá que calcular la segunda derivada, sustituir el punto candidato y ver el signo del valor que se obtiene para afirmar si es o no la solución deseada.
Pero ojo, también habrá que observar el contexto en el que nos estamos moviendo, y es que, si en el contexto del problema, la variable x sólo puede tomar valores dentro de un intervalo, hay que evaluar los valores extremos del intervalo, por si da la casualidad que ahí es donde se alcanza el máximo o el mínimo.
Lo vemos con nuestro ejemplo.
Para comprobar que un valor candidato es solución de un problema de optimización, hay que proceder así:
- Calcular la segunda derivada de la función.
- Sustituir el valor candidato en esa segunda derivada. Si sale una cantidad positiva es un mínimo relativo y si sale negativa un máximo relativo.
- Determinar el verdadero dominio de la función teniendo en cuenta el contexto del problema.
- Evaluar en la función inicial los valores extremos obtenidos y compararlos con los máximos o mínimos relativos
|
x= 2 y x= -4 son máximos relativos
| |
|
x= -2 y x=4 son mínimos relativos
| |
|
x= 2 es un máximo realtivo y x = -4 un mínimo
| |
|
x=2 es un mínimo relativo y x = -4 un máximo.
|
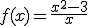 , el máximo relativo es:
, el máximo relativo es:
|
-1
| |
|
3
| |
|
-1 y 3
| |
|
No hay máximos relativos
|