2. Llevándolo al extremo.
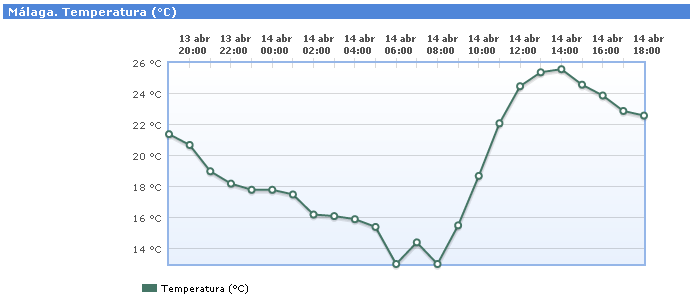
- La temperatura máxima se alcanza a las 14h del 14 de abril (25,6ºC)
- La temperatura mínima se alcanza a las 6h y a las 8h del 14 de abril (13ºC)
- A las 7h del 14 de abril hay un máximo relativo, pues es la temperatura más alta en un pequeño periodo de tiempo (de las 6 a las 8h).
Para poder averiguar la temperatura máxima o mínima necesitamos una tabla de datos observados o una gráfica como la anterior, pues la temperatura local no la podemos expresar con una función derivable.
Veamos por tanto qué ocurre en la siguiente función, y comparemos con su derivada:
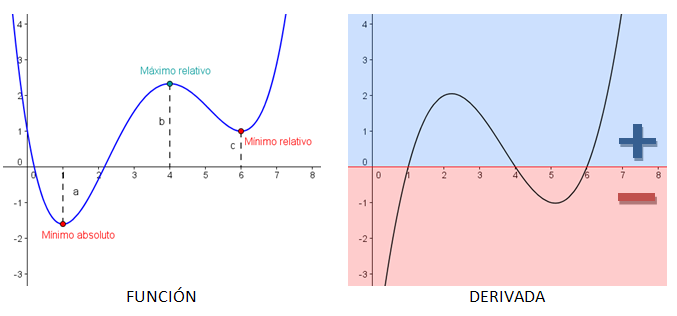
A la izquierda tenemos una función f(x) y a la derecha su derivada f '(x).
- Mínimo: si te fijas en los dos mínimos, a su izquierda la función es decreciente y a la derecha es creciente ¿qué quiere decir eso para la derivada? Como vimos en el apartado anterior, equivale a que a la izquierda la derivada es negativa y a la derecha positiva (como puedes ver en la gráfica de la derivada). Pues si en ese punto la derivada pasa de negativa a positiva, quiere decir que debe ser nula.
- Máximo: en el máximo pasa algo parecido, pero en este caso pasamos de función creciente a decreciente, es decir, de derivada positiva a negativa. Al igual que antes, en ese punto la derivada debe ser nula.
Una función f, continua y derivable en un intervalo (a,b), alcanza sus máximos y mínimos relativos en los puntos del intervalo (a,b) en los que f '(x)=0. Además, si estudiamos la segunda derivada:
- Máximo relativo: f '(x)=0 y f ''(x)<0.
- Mínimo relativo: f '(x)=0 y f ''(x)>0.
Para que veas cómo podemos hallar máximos y mínimos con la derivada, mira el siguiente ejercicio resuelto.
Una conocida compañía de telefonía va a poner a la venta un nuevo modelo de teléfono móvil para el que
prevé unas ventas para los primeros años que vienen dadas por la
función 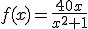 , donde x es el número de meses transcurridos desde que se saca a la venta y f(x) se mide en millones de unidades vendidas.
, donde x es el número de meses transcurridos desde que se saca a la venta y f(x) se mide en millones de unidades vendidas.
a) Determina los posibles máximos o mínimos de la función.
x = -1
| |
x = 0
| |
x = 1
| |
x = 2
| |
Al ponerlo en venta | |
El primer mes
| |
El segundo mes
| |
No es un dato necesario para la empresa
| |
El punto en el que se alcanza no pertenece al dominio del problema
| |
El punto en el que se alcanza no pertenece al dominio de la función
| |
10 millones de unidades
| |
20 millones de unidades
| |
40 millones de unidades
| |