1.1. Lluvia, vapor y velocidad
En la pintura se puede ver cómo un tren de vapor atraviesa un puente bajo una espesa lluvia.
Podemos estar casi seguros de que estos trenes no estaban dotados de velocímetros como los turismos actuales. Cuando circulamos en un coche podemos mirar en cualquier momento la
velocidad que marca el velocímetro y decimos "en este momento voy a
110 km/h", ¿pero qué ocurría con las locomotoras de vapor? Muy sencillo, recurrían al cálculo manual y estudiaban el espacio recorrido, y el tiempo que tardaban en recorrerlo. Pero estos cálculos dan lugar a una velocidad media entre dos instantes del viaje.
Este concepto se puede generalizar en matemáticas y como antes se ha mencionado, está relacionado con el comportamiento de las funciones en un intervalo.
Geométricamente, la tasa de variación media de la función f en el intervalo [a,b] es la pendiente de la recta secante a la gráfica de f que pasa por los puntos (a,f(a)) y (b,f(b)).
¿Pero, qué podemos hacer si queremos saber la velocidad en un momento concreto? Por ejemplo, la velocidad instantánea cuando paso por una estación sin para en ella. Si queremos definirla a partir de esa misma relación espacio recorrido y tiempo empleado en recorrerlo, tenemos un problema porque ese tiempo sería cero y el espacio también.
Sin embargo podemos recurrir a la idea de considerar las velocidades con que hemos recorrido trayectos cada vez más pequeños. Parece razonable que, si esos trayectos se van acortando hasta cero, las velocidades medias se irán aproximando a la velocidad con que viajo en ese instante determinado.
Volvamos atrás a nuestro video y a las imágenes de las gotas de agua. Si lo vemos de nuevo, podemos comprobar que a menor número de fps, la grabación es cada vez más rápida. Es decir, si nos acercamos lo máximo posible a 0, nuestra grabación se convertiría prácticamente en una fotografía de un instante.
Si ahora volvemos a las funciones y, teniendo en cuenta que b es mayor que a, se puede expresar b como a+h, donde h sería un número real y positivo, y de esta forma la tasa de variación media se podría expresar con la siguiente fórmula:
Si h se aproxima a cero, el punto b=a+h se aproximará al punto a y la tasa de variación media tenderá entonces a un valor que denominamos tasa de variación instánea de la función f en el punto a. Que si hablamos en términos de velocidad, sería justo la que marca el velocímetro de nuestro coche en un determinado momento.
 viene dada por:
viene dada por:
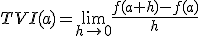
Calcula la tasa de variación instantánea de la función f(x)=x2 en x=2