1.2. ¿Qué ocurre si tenemos varias inecuaciones?
 |
| Fotografía en Flickr de marcp_dmoz bajo licencia Creative Commons |
Hasta ahora, habrás comprobado, y seguramente recordado, que esto de las inecuaciones no tiene mucha dificultad.
Hemos visto que fácilmente se nos presentan inecuaciones en situaciones cotidianas, pero lo más común es que se presenten varias en una misma situación, es decir, que en vez de una, tengamos un sistema de inecuaciones.
Por ejemplo, Pedro sólo tenía 10 € para gasolina, pero es que en esa gasolinera, lo mínimo que surtía era 2 litros, con lo cual ya aparecen dos desigualdades.
Quiere comprar mortadela, pero como mínimo tiene que pedir 100 gramos.
Y, de la misma forma que pasa con los sistemas de ecuaciones, puedes encontrarte con situaciones donde no hay solución. Imagina que lo mínimo que despacha la tienda es 1/4 y sólo tienes 1 €, como el Kg cuesta 5,70 €, no hay solución posible.
Escribe las dos inecuaciones que representan el problema de la gasolina, que acabamos de mencionar.
¿Cuál será la solución?
Vamos a resolver los siguientes sistemas de inecuaciones
a) 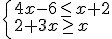
b) 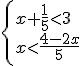
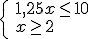

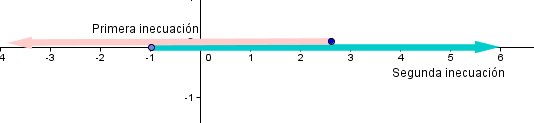
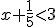
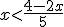
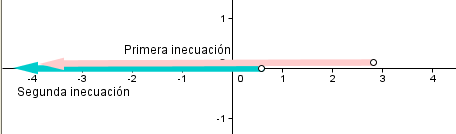
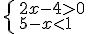 es (2,4).
es (2,4).

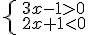 no tiene solución.
no tiene solución.