3.2. Los puentes de Königsberg
Königsberg, actualmente llamada Kaliningrado, es una ciudad que se encuentra a orillas del Mar Báltico, en territorio ruso y a unos 50 kilómetros de la frontera con Polonia.
Fue una ciudad que sufrió duros ataques durante las dos guerras mundiales, con lo cual podéis imaginaros los graves daños que se produjeron.
Muchos de sus edificios históricos fueron derrumbados por bombardeos. En 1946, en la Conferencia de Berlín, la ciudad pasó a manos de la antigua URSS, que le cambió el nombre, un año después, por el de Kaliningrado.
Además de Kant, en esta ciudad nacieron destacados científicos de los 3 últimos siglos, como son el físico Kirchoff y el matemático Hilbert.
Hilbert recibió muchos honores y en 1930 estando ya retirado, la ciudad de Königsberg le hizo ciudadano de honor. Son famosas sus palabras en las que se reconoce su entusiasmo por las matemáticas: "Debemos saber, así que sabremos". Estas mismas palabras se escribieron en su epitafio.
En el siglo XVII la ciudad de Königsberg estaba atravesada por el río Pregel que se dividía en el Viejo y en el NuevoPregel. Este río formaba dos islas a su paso por la ciudad, una de las cuales, la más pequeña, se llamaba la isla Kneiphof.
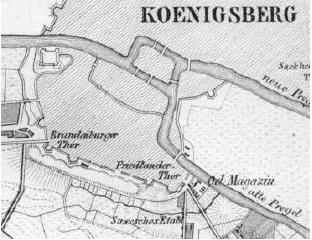 |
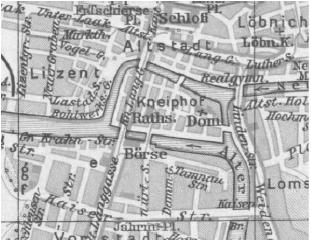 |
| Königsberg en tiempos de Euler | Kaliningrado. Siglo XX |
Para unir las cuatro partes de la ciudad separadas por la geografía, existían siete puentes.
Applet Descartes realizada por Salvador Calvo-Fernández Pérez bajo licencia Creative Commons.
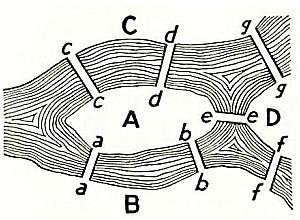 |
Hay siete puentes a, b, c, d, e, f y g, que cruzan por los dos brazos el río. La cuestión consiste en determinar si una persona puede realizar un paseo de tal forma que cruce cada uno de estos puentes sólo una vez”.
Este artículo es considerado por varios autores como el nacimiento de la Teoría de Grafos, utilizada actualmente en una gran cantidad de aplicaciones, y también como una de las primeras manifestaciones de una nueva Geometría.
La Teoría de Grafos permite la resolución de problemas relativos a campos tan separados como puedan ser la lingüística, la investigación operativa, la electricidad, la genética, la sociología, etc.
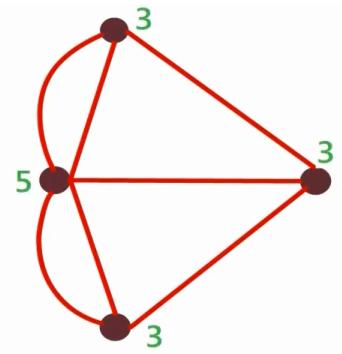
Un grafo consiste en un conjunto finito de vértices (puntos) y un conjunto finito de aristas (líneas) entre ellos.En un grafo, dos vértices se dicen adyacentes si ambos son extremos de una arista.
Toda arista es incidente con sus vértices extremos y dos aristas se dicen incidentes si ambas comparten un vértice común.
Se denomina valencia (o grado) de un vértice al número de vértices adyacentes con él o bien al número de aristas incidentes con él. Por convenio, un vértice no se considera adyacente consigo mismo y los vértices de valencia 0 se denominan vértices aislados.
Un camino en un grafo es una sucesión consecutiva de vértices y aristas del grafo, comenzando por un vértice, del tipo v1, e1, v2, e2, ..., vr-1, er, de tal manera que cada arista ei una los vértices vi-1 y vi.
Un camino euleriano sobre un grafo contiene cada arista del grafo una y sólo una vez.
Euler probó que el grafo de Königsberg no posee un camino eureliano.
En 1875 los alemanes construyeron un nuevo puente en la ciudad de Königsberg, situado entre las zonas B y C.
¿Es posible ahora planificar un paseo tal que se crucen los ocho puentes sin pasar por ninguno más de una vez?
Dibuja el grafo asociado para que te resulte más fácil resolver el problema.
- Puente de la Barqueta.
- Puente del Cristo de la Expiración.
- Puente de Isabel II, también conocido como puente de Triana.
- Puente de San Telmo.
- Puente de los Remedios.
- Puente de las Delicias
- Puente del V Centenario.
Ver Puentes de Sevilla en un mapa más grande




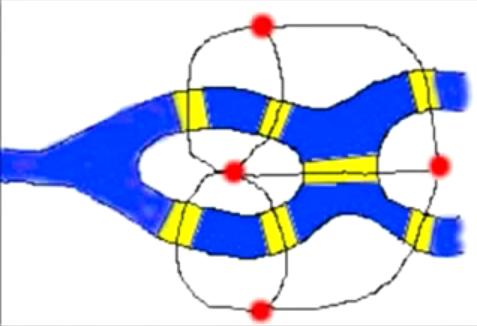
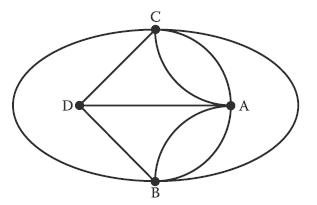 En la escena de la parte inferior, creada por
En la escena de la parte inferior, creada por