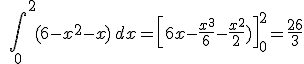4. Selectividad
Aquí puedes encontrar varios ejercicios propuestos en las pruebas de acceso a la universidad y relacionados con el tema en curso. Espero que te sean de mucha ayuda.
La gráfica de la función f de la figura corresponde a una función polinómica de grado 2.
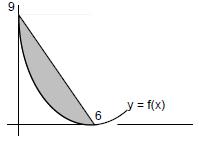 |
(1) [1’5 puntos] Determina una expresión algebraica de la función f.
(2) [1 punto] Calcula el área de la región sombreada.
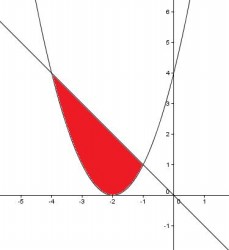
Dibuja y calcula el área del recinto limitado por la recta y+x = 0 y la curva de ecuación y = x2 + 4x + 4.
EJERCICIO
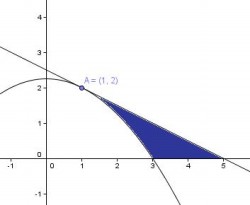
(a) [1 punto] Dibuja el recinto limitado por la curva 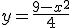 , la recta tangente a esta curva en el punto de abscisa x = 1 y el eje de abscisas.
, la recta tangente a esta curva en el punto de abscisa x = 1 y el eje de abscisas.
(b) [1’5 puntos] Calcula el área del recinto considerado en el apartado anterior.
Calcula el valor de 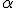 , positivo, para que el área encerrada entre la curva
, positivo, para que el área encerrada entre la curva 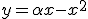 y el eje de abscisas sea 36.
y el eje de abscisas sea 36.
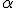 , positivo, para que el área encerrada entre la curva
, positivo, para que el área encerrada entre la curva 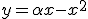 y el eje de abscisas sea 36.
y el eje de abscisas sea 36.
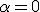
| |
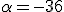
| |
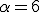
| |
|
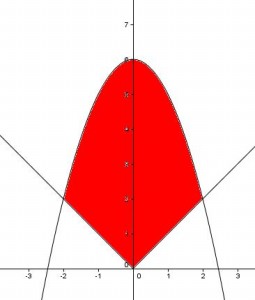
Considera las funciones f, g, funciones reales f(x) = 6 − x2, g(x) = |x|, con x real
(a) [1 punto] Dibuja el recinto limitado por las gráficas de f y g.
(b) [1’5 puntos] Calcula el área del recinto descrito en el apartado anterior.
(a) [1 punto] Dibuja el recinto limitado por las gráficas de f y g.
(b) [1’5 puntos] Calcula el área del recinto descrito en el apartado anterior.
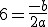 , donde la ecuación de la función será ax2+bx+c. Si la función pasa por el punto (0,9), sustituyendo obtenemos a*02+b*0+c=9,
por lo que c= 9. Por último sabemos también que la función pasa por el
punto (6,0).
, donde la ecuación de la función será ax2+bx+c. Si la función pasa por el punto (0,9), sustituyendo obtenemos a*02+b*0+c=9,
por lo que c= 9. Por último sabemos también que la función pasa por el
punto (6,0).
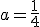 , b= -3 y c=9.
, b= -3 y c=9.
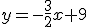 . Así, el área engendrada por ambas funciones sera
. Así, el área engendrada por ambas funciones sera 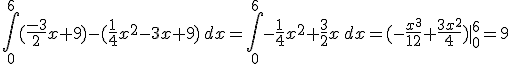
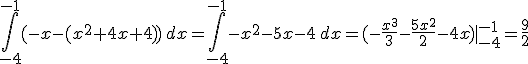
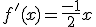 , por lo que la pendiente de la recta tangente será
, por lo que la pendiente de la recta tangente será 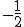 . Imponiendo que pase por el punto (1,2) obtenemos que la recta es
. Imponiendo que pase por el punto (1,2) obtenemos que la recta es 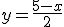
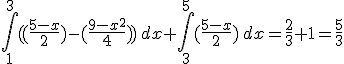
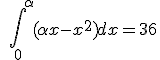 .
.