2.2. Envasando volumenes
Una vez obtenida la función a optimizar, debemos:
1. Determinar el dominio de la función a optimizar [a,b]
2. Calcular la derivada de la función f(x), f '(x)
3. Resolver la ecuación f '(x) = 0, donde obtendremos la soluciones x1,x2,x3,...
4. Calcular los valores f(a), f(x1),f(x2),f(x3),...,f(b)
5. Determinar aquellos valores para los que la función se hace máxima ó mínima.

Ángela ha comprado un pequeño terreno para plantar diversas vegetales y hortalizas. Quiere delimitar el terreno formando un rectángulo con un rollo de cuerda que mide 20 metros, de tal forma que la superficie que englobe sea máxima para así poder plantar más.
¿Cual será la función, de una sola variable, que determina el área encerrada? ¿Cuál sería la superficie máxima encerrada?
En primer lugar, vamos a determinar claramente la función solicitada. El problema nos indica que debemos trabajar con el área de un rectángulo y sabemos que el área de éste es base por altura es decir f(x,y)=x·y, donde x representa la base e y la altura.
Pero esta función tiene dos variables y pretendemos que nuestra función
solo tenga una variable. ¿De donde podemos obtener una condición para
eliminar una incógnita? Si leemos el problema, apreciamos una
condición, el rectángulo debe ser formado por una cuerda de 20 metros.
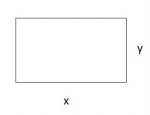
Esta condición, la pasaremos ahora a lenguaje algebraico, ya que la suma de los cuatro lados del rectángulo deben sumar 20 metros luego x + y + x + y = 20, es decir, 2·x + 2·y = 20. Despejando la variable y de esta expresión, determinamos que y = 10-x. En este momento, podemos ya sustituir nuestra variable y en la función f(x,y) de dos variables y obtener la función de una variable, la añorada f(x) = x·(10-x).
En el siguiente applets, creado por José Manuel Sánchez Grande, para el proyecto Descartes, puedes modificar el punto rojo y observaras el área que engloba el rectángulo en función del tamaño de la base.

|
| Foto tomada del Banco de imágenes de wikipedia. |
La empresa de conservas de tomates "Tomatori" necesita disminuir sus costes para salir de una dificil situación económica. Para ello, plantea a su suministrador de envases crear un nuevo recipiente de hojalata de 1 litro de capacidad, pero disminuyendo los costes lo máximo posible.
Desde la empresa de recipientes, plantean la construcción del nuevo recipiente, pero desconocen cuáles deben ser las medidas del radio y la altura del cilindro para gastar la menor cantidad de hojalata en su construcción y que el volumen sea 1 litro, lo deseado por el cliente.
Indica cuales deben ser el radio y la altura del envase buscado.
 |
| Foto del Banco de Imágenes de wikipedia. |
Una conocida cadena de grandes almacenes, "El Corte Escocés" quiere lanzar para su campaña de Navidad unas pequeñas cajas cuadradas con tapas para envolver regalos.
Pretenden que la capacidad sea 8 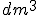 , pero que el coste sea el más económico.
, pero que el coste sea el más económico.
Indica las dimensiones que debe tener la caja para que la superficie exterior sea mínima.
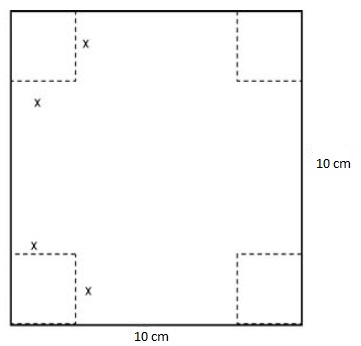 En primer lugar, debemos construir la función que proporciona el volumen de la caja. Al ser el volumen el de un prisma cuadrangular, (área del cuadrado de la base por la altura), podemos afirmar que la función que obtiene el volumen de la caja es V(x) = (10-2x)·(10-2x)·x, es decir V(x) = 4x3-40x2+100x, definida entre x en [0,5] ya que son los valores que puede tomar la variable independiente
En primer lugar, debemos construir la función que proporciona el volumen de la caja. Al ser el volumen el de un prisma cuadrangular, (área del cuadrado de la base por la altura), podemos afirmar que la función que obtiene el volumen de la caja es V(x) = (10-2x)·(10-2x)·x, es decir V(x) = 4x3-40x2+100x, definida entre x en [0,5] ya que son los valores que puede tomar la variable independiente
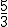 .
.
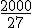
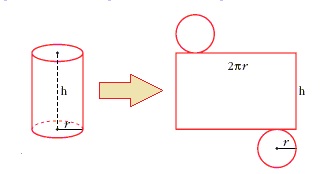 Veamos en primer lugar la relación entre el volumen y el área.
Veamos en primer lugar la relación entre el volumen y el área.
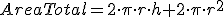
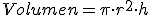 y pretendemos que el volumen sea 1 litro =1
y pretendemos que el volumen sea 1 litro =1 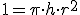 y la relación entre radio y altura es
y la relación entre radio y altura es 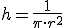 . Sustituyendo ahora en la función del AreaTotal, obtenemos
. Sustituyendo ahora en la función del AreaTotal, obtenemos
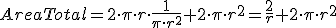
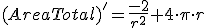
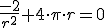 , obtenemos
, obtenemos 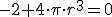 y
y 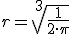
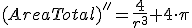
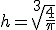 dm.
dm.
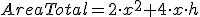 .
.
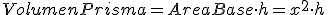 .
.
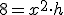 ,
, 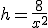 .
.
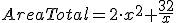
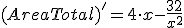 y resolviendo la ecuación
y resolviendo la ecuación 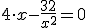 obtenemos un valor crítico, x =2
obtenemos un valor crítico, x =2
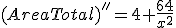 , observamos que el valor crítico es un mínimo.
, observamos que el valor crítico es un mínimo.