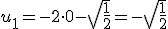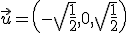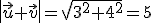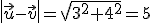3.1. Ejercicios
Si 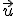 y
y 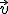 son dos vectores, demostrar que
son dos vectores, demostrar que 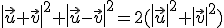
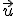 y
y 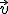 son dos vectores, demostrar que
son dos vectores, demostrar que 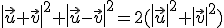
Considera los vectores 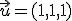 ,
, 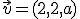 y
y 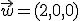
1.- Halla los valores de  para los que los tres vectores son linealmente independientes.
para los que los tres vectores son linealmente independientes.
2.-Determina los valores de  para los que los vectores
para los que los vectores 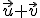 y
y 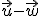 son ortogonales.
son ortogonales.
Calcula un vector de módulo 1 que sea ortogonal a los vectores (1,0,2) y (2,0,1)
Halla dos vectores linealmente independientes que sean ortogonales al vector 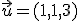
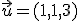
Escribe un vector de módulo 1 que sea ortogonal al vector 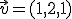
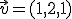
Sean 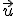 y
y 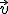 dos vectores ortogonales de módulo 4 y 3 respectivamente. Calcula el módulo de los vectores
dos vectores ortogonales de módulo 4 y 3 respectivamente. Calcula el módulo de los vectores 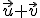 y
y 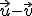
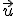 y
y 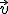 dos vectores ortogonales de módulo 4 y 3 respectivamente. Calcula el módulo de los vectores
dos vectores ortogonales de módulo 4 y 3 respectivamente. Calcula el módulo de los vectores 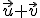 y
y 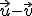
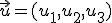 y
y 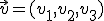 entonces:
entonces:
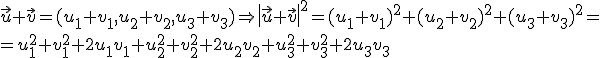
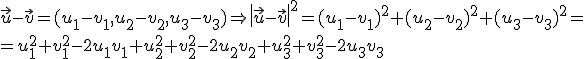
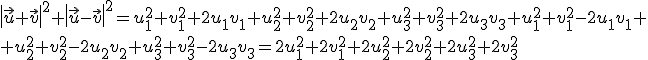
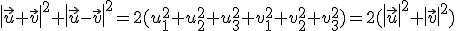
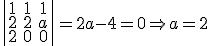
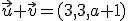 y
y 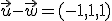 son ortogonales si su producto escalar es cero, es decir:
son ortogonales si su producto escalar es cero, es decir:
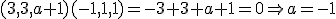
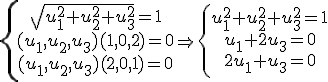
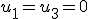 , por lo que sustituyendo en la primera tenemos que:
, por lo que sustituyendo en la primera tenemos que:
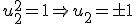 . Así, tenemos dos soluciones:
. Así, tenemos dos soluciones:
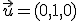 y
y 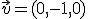
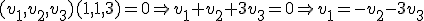
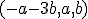 Así, basta tomar dos vectores
Así, basta tomar dos vectores 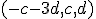 de forma que la matriz formada por ellos tenga rango 2. Por ejemplo, en nuestro caso
de forma que la matriz formada por ellos tenga rango 2. Por ejemplo, en nuestro caso
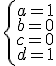 Los vectores que resultan son (-1,1,0) y (-3,0,1)
Los vectores que resultan son (-1,1,0) y (-3,0,1)
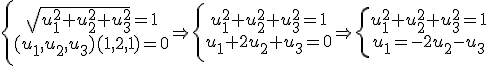
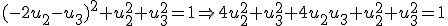 Como se trata de encontrar un vector, si hacemos
Como se trata de encontrar un vector, si hacemos 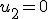 tenemos que
tenemos que
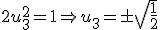 Si tomamos la positiva y sustituimos en la segunda ecuación del sistema tenemos que:
Si tomamos la positiva y sustituimos en la segunda ecuación del sistema tenemos que: