2. Con tablas se entiende...

Colorful de Zentra con licencia by-nc-sa-2.0

Countdown to zero de Zentra con licencia by-nc-sa-2.0

 

De una cantidad de datos sin orden, ¿podemos obtener alguna información?

Parece lógico pensar que ordenándolos y posteriormente encontrando semejanzas podamos agruparlos y obtener, de esta forma, una información que pueda describirnos la población escogida.

La manera habitual de trabajar es colocar los datos en tablas que indiquen el número de veces que se repite cada modalidad, estas tablas se llaman tablas de frecuencias.
 
Ahora bien no es lo mismo que una modalidad se repita 5 veces en un total de 50 datos que en un total de 500. Por tanto, hablaremos de frecuencias absoluta y relativa.
 
Por ejemplo, en una de las encuestas que aparecía en la autoevaluación del apartado anterior, la que se preguntaba por el prespuesto en euros que se diponía para Semana Santa, tuvo un total de 605 repuestas. En la siguiente tabla aparecen las frecuencias absolutas y relativas que tuvieron cada una de las respuestas posibles.
 
Variable frecuencia absoluta
 frecuencia relativa frecuencia relativa (en %)
0 206 0,34 34
menos de 100
 139 0,23 23
entre 100 y 300
 139 0,18 18
más de 300
 151 0,25 25
TOTAL 605 1 100
Icono IDevice Actividad

La frecuencia absoluta es el número de veces que se repite una modalidad de una variable en un estudio estadístico. Se suele representar por ni.

La frecuencia relativa es el cociente entre la frecuencia absoluta (ni) y el número total de datos (N). Se representa por fi.

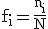
La suma de todas las frecuencias absolutas es igual al número total de datos (N).

Y por tanto, la suma de todas las frecuencias relativas es 1.

Por último, añadir que multiplicando las frecuencias relativas por 100, obtenemos el tanto por ciento de esa modalidad en la muestra.

 


Icono IDevice Pre-conocimiento
La frecuencia relativa es la proporción de datos en los que aparece una modalidad. En cierto modo, se corresponde con la probabilidad de que se dé esa modalidad. Esto es lo que se conoce como enfoque frecuentista de la probabilidad.
 
 
 
 
 
 
 
Como has podido ver C3PO, el androide más famoso del cine, es un entusiasta de los datos y les insinúa a sus compañeros que sólo 1 nave de 3750, ha conseguido pasar el campo de asteroides, es decir, hace un enfoque frecuentista de la probabilidad.

En multitud de ocasiones nos interesa agrupar los datos de manera que sin perder información nos sean más útiles.
 
 

Panneau-dormir de Liquid_2003

con licencia cc by-sa-3.0

 
 
 
Volviendo al ejemplo del tiempo, es interesante conocer en cuántas provincias se puede dormir en verano, es decir, cuántas están por debajo del umbral del sueño.
 
Cogiendo los datos del video de la página anterior, que se refieren a las temperaturas de una sola noche, obtenemos la siguiente tabla:
 
Temperaturas ni Ni
15ºC 1 1
16ºC 3 4
17ºC 4 8
18ºC 2 10
19ºC 3 13
20ºC 1 14
21ºC 5 19
22ºC 6 25
23ºC 2 27
24ºC 2 29
 
Sabiendo que para poder conciliar el sueño necesitamos una temperatura inferior a 22ºC, de la tabla anterior se deduce que sólo en 19 de las provincias estudiadas han dormido a pierna suelta.
 
La tercera columna de la tabla hace referencia al concepto de frecuencia absoluta acumulada.
Icono IDevice Actividad

La frecuencia absoluta acumulada es el resultado de sumar la frecuencia absoluta de una modalidad de la variable con todas las frecuencias de las modalidades anteriores.

En consecuencia, las frecuencias relativas acumuladas representa la proporción de individuos de una muestra que presentan alguna de las i primeras modalidades.
 
La última frecuencia absoluta acumulada es igual al número total de datos.
 
Y por tanto, la última frecuencia relativa acumulada es igual a 1.

Cuando la variable es cuantitativa continua se utiliza la técnica de construir intervalos de clase, en los cuales se agruparán los datos observados en una muestra. Así, cada intervalo es considerado como una modalidad, tomándose como frecuencia absoluta de cada modalidad el número de observaciones agrupadas en el intervalo correspondiente.
 
Una vez construidos los intervalos de clase, se elige un representante de cada uno de ellos, llamado marca de clase, que normalmente es el punto medio del intervalo.
 
Pero veamos todo esto con el siguiente ejercicio resuelto en el que construiremos una tabla de frecuencias para una variable cuantitativa continua.
Icono de iDevice Caso de estudio
En una biblioteca se ha realizado una encuesta entre los usuarios de los libros que se han leído en el último mes:
4,1,3,10,5,2,2,5,1,19,8,3,5,15,2,1,1,1,6,3,2,12,3,7,6,3,4,1,10,7,11,6,7,12,4,2,8,5,9,3,6,8,2,1,12,9,8,5,2,3,3,4,3,7,9,1,4,9,5,8,6,12,17,3,9,6,7,5,5,3,9,7,8,11,2.
Elaboraremos una tabla de frecuencias agrupando los valores en intervalos.

Icono de iDevice AV - Actividad de Espacios en Blanco
Ya sabes de la importancia que tiene en la actualidad seguir aprendiendo a lo largo de toda la vida. Podríamos afirmar que la formación continua está calando hondo cada vez más en nuestra sociedad.
 
Para justificar lo que acabamos de decir, observa los datos que aparecen en la siguiente tabla extraída de la Encuesta sobre la Participación de la Población Adulta en las Actividades de Aprendizaje (EADA) 2007, realizada por el Instituto Nacional de Estadística (INE), en la población española de edad comprendida entre 25 y 75 años.
Algunos datos aparecen en blanco. ¿Podrías completarlos?

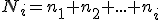
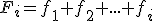
Tramos de edad

(en años)

Marca de clase

Número de personas que participan

en actividades formativas, ni

Frecuencia absoluta

acumulada, Ni

Frecuencia relativa

acumulada, Fi

[25, 35)
 30 3.018.026 3.018.026
 0,37
[35, 45) 2.433.843

[45, 55) 50 1.624.953 7.076.822
 0,87
[55, 65) 7.882.197
 0,96
[65, ) 70 298.697

TOTAL   8.180.894    
  

« Anterior | Siguiente »