1. Sin sobresaltos
 |
| huellas y trazas de TwOsE, CC by-nc 2.0 |
¡Qué extraños somos los humanos! Nunca sabemos bien a qué carta jugar. Por un lado nos gusta una vida tranquila, sin sobresaltos. Preferimos los cambios suaves, sin asperezas, que haya una cierta continuidad en nuestra experiencia vital. Pero, por otro lado, solemos acabar aburriéndonos si nuestra existencia no está salpicada de acontecimientos que nos hacen darnos cuenta de que estamos vivos. Un encuentro inesperado, una conversación breve que cambia el rumbo de nuestras vidas. Momentos que significaron un salto en nuestra pequeña historia íntima y que pasado el tiempo, son los que nos quedan fijos en el recuerdo de ese discurrir continuo y aburrido.
¿Continuidad o no? Esa es la cuestión.
Podemos encontrar analogías a la reflexión anterior en el ámbito de las funciones. La continuidad es la situación más común, y la discontinuidad lo que más llama la atención.
En la siguiente escena de GeoGebra podemos ver ocho funciones de las estudiadas en la Unidad anterior. Casi todas ellas son continuas. Sólo hay dos con ... sobresaltos.
Si mueves el punto rojo irás cambiando de función, si mueves el naranja podrás recorrer la gráfica de las funciones de forma continua, o no.
Actividad
AV - Actividad de Espacios en Blanco
y .
(Debes escribir las letras en orden alfabético).
Actividad
Una función f se dice continua en un punto a, si f(x) se aproxima a f(a) cuando x se acerca a a.
En caso contrario, la función se dirá discontinua en dicho punto.
Una función que es continua en todos los puntos que está definida, se dirá continua.
Casi todas las funciones elementales que estudiamos en la Unidad anterior son continuas en su dominio.
Las funciones lineales, cuadráticas y polinómicas en general, son continuas en todo su dominio.
Las funciones de proporcionalidad inversa y las racionales en general, son continuas en todo su dominio. Es decir, son continuas menos en los puntos donde se anula el denominador de la función.
Las funciones exponenciales, logarítmicas y trigonométricas, también son continuas en su dominio. Por ejemplo, la función tg(x) no es continua en los puntos donde el coseno es 0. Pero dichos puntos no pertenecen a su dominio.
La mayoría de las funciones que no son continuas se encuentran entre las funciones definidas a trozos.
En la siguiente escena de GeoGebra vamos a estudiar la continuidad de cuatro funciones diferentes en el punto a=2. El punto verde se utiliza para cambiar de función, y el naranja para acercarnos al punto 2, tanto para valores menores como mayores que 2. Mira con detenimiento qué ocurre con f(x) cuando x se acerca a 2. De ese modo podrás deducir si la función es continua o no en 2.
AV - Reflexión
 |
| Fotografía perteneciente al Banco de imágenes de ITE |
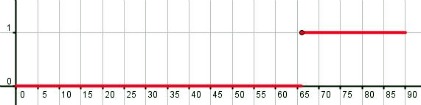
El partido de la primera división española, jugado el 10 de abril de 2011 entre el Gijón y el Osasuna, terminó con un 1-0, siendo Barral, jugador del Sporting, quien marcó el único tanto del encuentro en el minuto 66.
Está claro que uno de los instantes que quedará para el recuerdo de los aficionados gijoneses será ese minuto en que su equipo marcó el gol. Casi todo el resto del partido quedará en el olvido.
Consideramos la función que asocia a cada uno de los 90 minutos que dura el partido, los goles que se han marcado hasta ese momento.
Representa la gráfica de dicha función, y di si es continua o no. ¿Cuál es el punto de discontinuidad? ¿Y el motivo de la discontinuidad en ese punto?
Pre-conocimiento
Ya comentamos en la Unidad anterior que el concepto de función tardó siglos en construirse. Para recordar cómo fue esa historia puedes ver una presentación en el siguiente enlace: breve historia de las funciones.
La definición de continuidad de una función es una cuestión de los siglos XIX y XX. En los dos siglos anteriores, las funciones estaban determinadas por curvas o por su expresión analítica. Y todas eran continuas. Fue a principios del XIX cuando matemáticos como Fourier, piensan que es necesario alejar la idea de función como una relación que viene dada por una fórmula.
A partir de entonces la veda queda abierta, y las posteriores definiciones permiten la aparición de funciones definidas a trozos o como límite de otro conjunto de funciones. Algunas de ellas podrían ser consideradas verdaderas patologías incluso para mentes muy abiertas como la de Euler.
Un ejemplo podría ser la función que se define de la siguiente manera: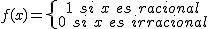 
. ¿Te imaginas cómo es su gráfica?