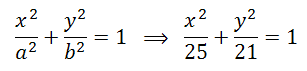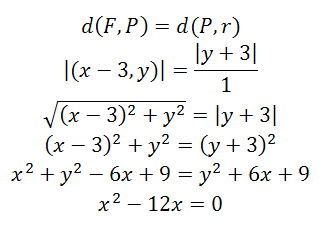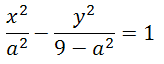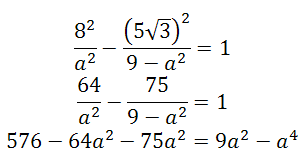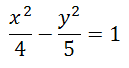4. Deconstrucción de cucurucho
|
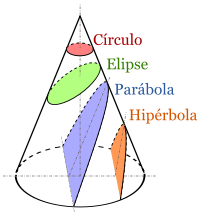
| Secciones cónicas, de Drini, CC 3.0 by-sa |
"En la época en la que Sinuhé recorría su camino por Egipto siguiendo las indicaciones de Eratóstenes, vivía en la ciudad de Alejandría otro gran matemático llamado Apolonio de Perga. Casualmente Sinuhé se lo encontró en un mercado, frente a un puesto de quesos. Aún cuando no sabía quién era, se quedó extrañado por la forma en que miraba uno de los quesos.
- ¿Os pasa algo señor? - preguntó Sinuhé.
- Es curioso cómo las matemáticas siguen apareciendo donde menos te lo esperas.
- Ciertamente es curioso, aunque si os referís a ese queso con forma de cono, se debe a la forma del recipiente donde se cuajó, no a la mano de la naturaleza.
- Veo que algo de matemáticas sabes, así que contéstame a esto: si corto paralelo a la base, ¿qué forma obtengo?
- Una circunferencia, es sencillo.
- Sí, y es una forma curiosa, pues todos sus puntos están a la misma distancia del centro. ¿Y si inclino un poco el corte?
- Sería una circunferencia algo aplastada ¿qué tiene eso de curioso?
- Yo llamo elipse a esa figura, y por supuesto que es curiosa. Hay dos puntos especiales dentro de ella. Si mides desde cualquier sitio del borde hasta esos dos puntos y sumas las cantidades, siempre obtendrás el mismo valor.
- Pero eso no puede ser siempre verdad, pues si inclino aún más el corte ya no tendré ninguna circunferencia aplastada.
- Elipse.
- Bueno... ninguna elipse - contestó Sinuhé, intentando buscar algún fallo en aquella teoría.
- Si haces eso, ya no tienes una elipse, sino una forma que yo llamo parábola y que también tiene una curiosa propiedad. - Dijo Apolonio sonriendo.
- ¿Y si corto verticalmente?
- Obtendrás una hipérbola... o al menos una parte de una hipérbola. Pero para explicártelo mejor te invito a que nos comamos este queso y sigamos razonando."
Curioso, ¿no? En el siguiente video tienes la explicación gráfica del comentario anterio (está en portugués, pero se entiende perfectamente).
En la siguiente aplicación, de José Antonio Cuadrado V. y que puedes visitar en la web del ITE, puedes ver las definiciones y propiedades de las secciones cónicas. Si pulsas en la esfera naranja verás la elipse, en la verde la parábola y en la morada la hipérbola. Tras la aplicación puedes hacer un ejercicio de autoevaluación para ver lo que has aprendido.
 Las respuestas a esta autoevaluación las tienes en la aplicación superior. Tan sólo tienes que centrarte en los puntos señalados en el esquema de la derecha para cada una de las secciones cónicas.
Las respuestas a esta autoevaluación las tienes en la aplicación superior. Tan sólo tienes que centrarte en los puntos señalados en el esquema de la derecha para cada una de las secciones cónicas.
Completa los huecos con la sección correcta: circunferencia, elipse, parábola o hipérbola.
a) Sección cónica: Si cortamos el cono con un plano...
- ... paralelo a una generatriz, se obtiene una .
- ... paralelo a dos generatrices, se obtiene una .
- ... que corta a todas las generatrices, se obtiene una .
b) Lugar geométrico: El lugar geométrico formado por todos los puntos del plano cuya...
- ... suma de distancias a otros dos puntos fijos llamados focos es constante, se llama .
- ... distancia a un punto fijo llamado centro es constante, se llama .
- ... resta de distancias a dos puntos fijos llamados focos es constante, se llama .
c) Parámetros:
- Una tiene foco y directriz.
- En una , c < a
- En una , c > a
d) Ecuación: La ecuación reducida de una...
- ...
es 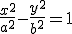
- ...
es 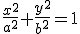
- ...
es 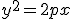
ELIPSES: Averigua la ecuación reducida de una elipse cuyos focos son los puntos F=(-2,0) y F'=(2,0), sabiendo que la longitud del eje mayor es 10.
Ayuda: intenta resolverlo a partir de los parámetros a, b y c de la elipse.
PARÁBOLAS: Halla el lugar geométrico de los puntos del plano que equidistan del punto F=(3,0) y de la recta d ≡ y+3=0.
Ayuda: Plantea la ecuación con la condición que se da en el problema.
HIPÉRBOLAS: Halla la ecuación de una hipérbola que tiene por focos los puntos F=(-3,0) y F'=(3,0), y que pasa por el punto P=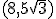
Ayuda: Escribe la ecuación reducida a partir de los focos y luego utiliza que el punto verifica la ecuación.