3. ¡Quién reparte se lleva la mejor parte!
|
|
Seguros en fracciones de etrinqita con licencia cc by-nc-nd-2.0 |
Pre-conocimiento
 |
|
Esfinge i Gran Piramide de Vulcano con licencia CC by-sa 3.0 |
Está documentado que los babilonios ya conocían y operaban con fracciones hacia el 2000 a.C. Su forma de representarlas era muy parecida a la actual, con la curiosidad de utilizar sólo las potencias de 60 como valores del denominador.
En el Papiro Rhind de los egipcios, hallamos fracciones propias, con la unidad como numerador (unitarias).
Las fracciones unitarias estaban escritas utilizando un símbolo en forma
de boca y el denominador debajo de este símbolo. Excepto para la
fracción 
que
tenía un símbolo especial, todas las otras fracciones con numerador
diferente a 1 las escribían como suma de fracciones unitarias.
Por ejemplo, en vez de 
escribían 
o para 
escribían 
.
En la actualidad, se ha llegado a la conclusión de que los hindúes escribían fracciones como lo hacemos hoy, pero sin la barra horizontal, elemento que fue invención árabe.
Actividad
En la actualidad, definimos fracción como el cociente entre dos números enteros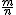 
, en donde n nunca puede ser cero.
Los enteros y las fracciones forman el conjunto de los números racionales, que representamos por Q.
Fracciones musicales
Ya sabes que para Pitágoras y sus seguidores todo podía ser expresado mediante número. Incluso la música.
En instrumentos de cuerda, como las arpas, se ha descubierto que hay una relación entre la longitud de las cuerdas y las notas que éstas producen al ser tocadas.
Por ejemplo, si una cuerda produce la nota SOL, otra de doble longitud dará también SOL, pero en otra octava.
Para conseguir el resto de las notas, ¿de qué longitud tiene que ser cada cuerda?
Los pitagóricos hallaron esas longitudes y las expresaron como fracciones que toman como referencia la cuerda más pequeña que produce la nota SOL.
Un arpa así construida tendría el aspecto que aparece en el dibujo.