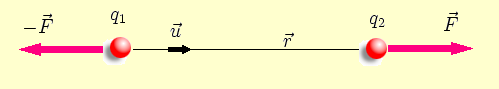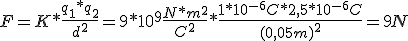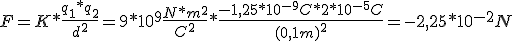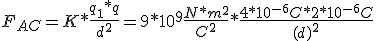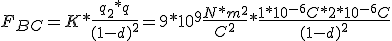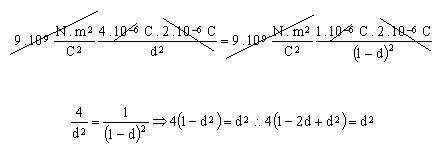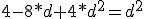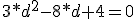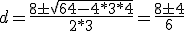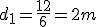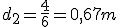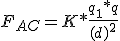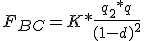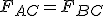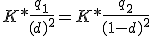2. Ley de Coulomb
Ya conocemos la composición de la materia, sus moléculas y la parte más pequeña, el átomo: El núcleo compuesto por protones (Carga positiva) y neutrones, y alrededor del mismo, orbitando, los electrones (carga negativa). Al ser cargas de distintos signos se atraen y los electrones se mantienen en sus órbitas debido a esas fuerzas de repulsión, girando sobre el mismo núcleo. Pero ¿sabéis que esas fuerzas se pueden medir? Sí, con una sencilla ley, La Ley de Coulomb. Veamos cómo.
 |
|
Imagen 2. Charles Augustin de Coulomb |
Actividad
LA LEY DE COULOMB
La fuerza F de acción recíproca entre cargas puntuales es directamente proporcional al producto de las cargas eléctricas (Q y Q') e inversamente proporcional al cuadrado de la distancia que las separa (d).
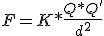
En el Sistema Internacional de Medidas (SI) y en el vacío, las unidades serían las siguientes:
- K es la constante de Coulomb y su valor se escribe en función de otra constante ξ0, que recibe el nombre de permitividad del vacío
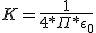
- Cargas Q y Q' en C (Culombios). Un Coulomb es el valor de una carga tal que repele a otra igual colocada a un metro de distancia con una fuerza de 9.109 N.
- Distancia d en m. (metros)
- En consecuencia la fuerza F se medirá en N (Newton).
Actividad
De lo anterior podemos deducir que la Ley de Coulomb se puede expresar:
Ejemplo o ejercicio resuelto
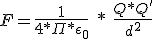
Determinar la fuerza que actúa sobre las cargas eléctricas Q1 = + 1 x 10-6 C. y Q2 = + 2,5 x 10-6 C que se encuentran en reposo y en el vacío a una distancia de 5 cm.
|
Ejemplo o ejercicio resuelto
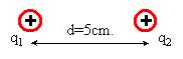
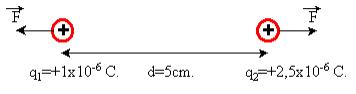
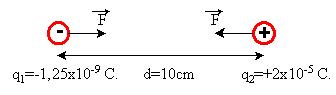
Determinar la fuerza que actúa sobre las cargas eléctricas q1 = -1,25 x 10-9 C. y q2 = +2 x 10-5 C. que se encuentran en reposo y en el vacío a una distancia de 10 cm.
 |
Ejemplo o ejercicio resuelto
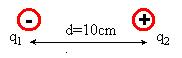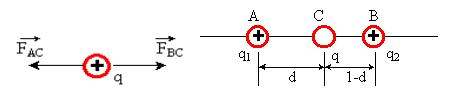
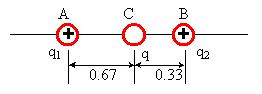
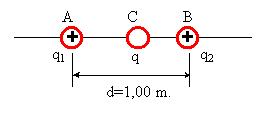
Supongamos un segmento AB de 1.00 m. de longitud sobre el que se fijan dos cargas. Sobre el punto A tenemos la carga q1 =+4 x 10-6C. y sobre el punto B situamos la carga q2=+1 x 10-6C.
a) determinar la posición de una tercera carga q=+2 x10-6C. colocada sobre el segmento AB de modo que quede en equilibrio bajo la acción simultánea de las dos cargas dadas.
b) La posición de q, ¿depende de su valor y signo?
|
