3.2. Cono y Pirámide
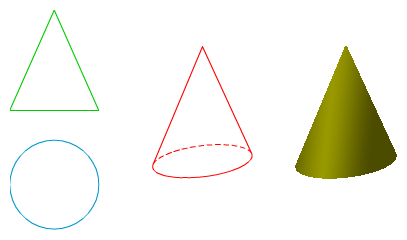
Las posiciones que puede ocupar un cono recto de revolución respecto de las caras del triedro pueden ser infinitas.
Como vimos en el cilindro, la perspectiva caballera de una circunferencia únicamente
se proyecta en verdadera magnitud, sin deformación, cuando es paralela
o está contenida en el plano XOZ, por tanto, nosotros solamente vamos a
analizar esta disposición.
En la imagen izquierda tienes la perspectiva caballera de un cono recto de revolución apoyado en el plano XOY, observa cómo su base es una elipse.
Cono recto de revolución. Su base es paralela al plano XOZ.
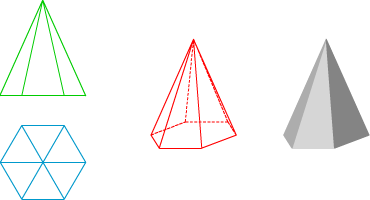
Las posiciones que una pirámide regular, considerando su base y su eje, respecto de las caras del triedro, pueden ser infinitas.
Nosotros solamente vamos a analizar aquellas posiciones en las que su base sea paralela a uno de los planos de proyección, y lógicamente su eje será perpendicular a dicho plano. Uno de los lados de la base, como mínimo, será paralelo a uno de los ejes isométricos.
La base puede estar contenida o no en las caras del triedro.
En la imagen izquierda tienes la perspectiva caballera de una pirámide regular, de base hexagonal, apoyada en el plano XOY, con dos lados paralelos al eje X
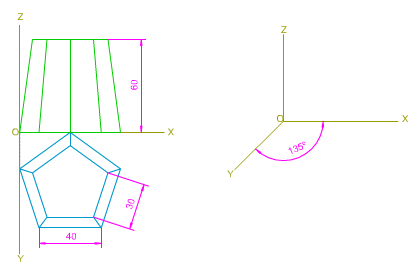 |
En la imagen izquierda tienes las vistas diédricas de una pirámide truncada de bases pentagonal, apoyada en el plano XOY por su base mayor, y uno de sus lados paralelo al eje X.
Tienes que dibujar las proyecciones secundarias y directa, determinado su perspectiva caballera.
|