2.1. Cilindro y Prisma
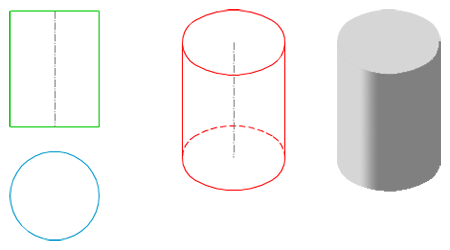
Las posiciones que puede ocupar un cilindro recto de revolución respecto de las caras del triedro pueden ser infinitas.
Nosotros solamente vamos a analizar aquellas posiciones en las que sus bases sean paralelas a uno de los planos de proyección.
Estas bases pueden estar contenidas o no en las caras del triedro.
En la imagen izquierda tienes la perspectiva isométrica de un cilindro apoyado en el plano XOY, observa cómo su base es un óvalo isométrico (o una elipse).
Posiciones del cilindro.
Una base está contenida en un plano del triedro y es tangente a las otras caras.
Dibujo isométrico de un cilindro.
En la animación inferior puedes ver cómo se ha realizado el dibujo isométrico de las proyecciones secundarias (planos XOY, XOZ) y directa de un cilindro cuyas bases son paralelas al plano XOY. Puedes ver cómo el cilindro no es tangente a ningún plano del triedro.
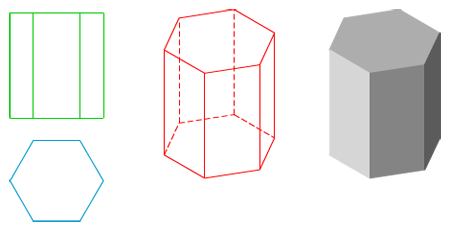
Las posiciones que puede ocupar un prisma regular respecto de las caras del triedro pueden ser infinitas.
Nosotros solamente vamos a analizar aquellas posiciones en las que sus bases sean paralelas a uno de los planos de proyección, y con al menos uno de los lados, de la otra base, paralelo a uno de los ejes isométricos.
Las bases pueden estar contenidas o no en las caras del triedro.
En la imagen izquierda tienes la perspectiva isométrica de un prisma regular, de base hexagonal, apoyado en el plano XOY, con dos lados paralelos a un eje isométrico.
Posiciones del prisma.
Una base está contenida en un plano del triedro. En este ejemplo la base hexagonal tiene dos lados paralelos a un eje isométrico.
Dibujo isométrico de un prisma.
En la animación inferior puedes ver cómo se ha realizado el dibujo isométrico de las proyecciones secundarias (planos XOY, XOZ) y directa de un prisma regular, cuyas bases, hexagonales, son paralelas al plano XOY. Puedes ver cómo ninguna arista del prisma está contenida en los planos del triedro.
Dibujo isométrico de un prisma seccionado.
En esta animación te mostramos un prisma regular de base hexagonal seccionado por la mitad mediante dos cortes, uno longitudinal y otro transversal.
Dicho prisma está apoyado en los planos de triedro:
- En el plano ZOY por una de sus bases.
- En el plano XOY por una de sus caras laterales.
- En el plano XOZ por una arista lateral.
El prisma queda definido por sus vistas diédricas alzado planta y perfil derecho.
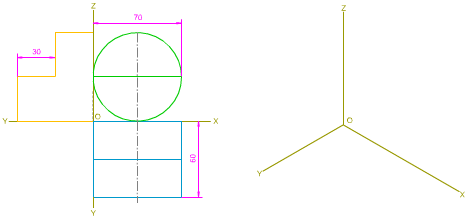 |
En la imagen izquierda tienes las vistas diédricas de un cono recto de revolución seccionado, apoyado por una de sus bases en el plano XOZ, y tangente a los planos XOY, ZOY. Tienes que trazar las proyecciones secundarias y directa, determinado su dibujo isométrico. |
Para realizar este ejercicio debes tener en cuenta los siguientes datos:
- Diámetro de las bases: 70 mm.
- Altura del cilindro: 60 mm.
- Sección: 30 x 30.