3.1 Triángulos y cuadriláteros
Comenzamos el estudio de las formas planas más sencillas: triángulos y cuadriláteros paralelogramos, estos últimos constituyen la base sobre la que trazaremos cualquier forma plana.
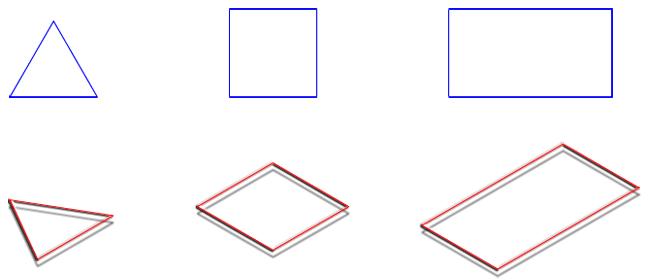
En la imagen superior tienes un ejemplo de dibujo isométrico de un triángulo equilátero, un cuadrado y un rectángulo.
En la imagen inferior tienes dos ejemplos de trazado isométrico de un triángulo equilátero, en un caso uno de los lados del triángulo es paralelo a un eje del sistema y en el otro está contenido en él.
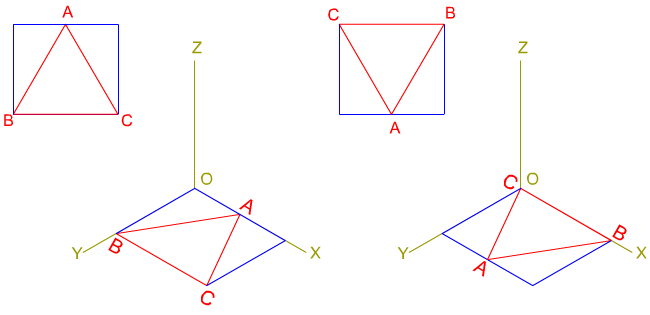
CUADRILÁTEROS. En la representación de cuadriláteros paralelogramos siempre los consideraremos con sus lados dispuestos de forma paralela a los ejes del sistema. En caso contrario tendremos que inscribirlo en otro paralelogramo.
Si tenemos que representar un rombo, romboide o cualquier cuadrilátero no paralelogramo (trapecios y trapezoides) lo inscribiremos en un paralelogramo cuadrado o rectángulo.
En la animación inferior puedes ver el dibujo isométrico de
un paralelogramos rectángulo cuyos lados son paralelos a los ejes del sistema. Observa
cómo ningún lado está contenido en los ejes isométricos.
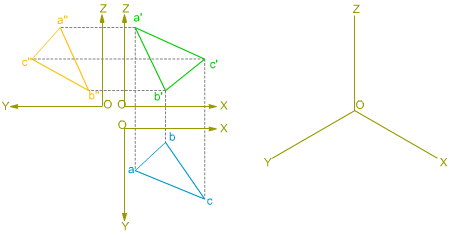 |
En la imagen izquierda tienes las proyecciones diédricas (alzado, planta y perfil derecho) de un triángulo ABC y los ejes isométricos XYZ; tienes que realizar el dibujo isométrico de dicho triángulo: proyecciones secundarias y directa. |