3.3. Plano
DISTANCIA DE UN PUNTO A UN PLANO.
La distancia de un punto a un plano queda determinada por el segmento perpendicular a dicho plano trazado desde el punto.
Este caso es muy importante ya que es fundamental para determinar la altura de superficies apoyadas en planos.
Para calcular la longitud de este segmento tenemos que determinar la intersección con el plano de la recta perpendicular trazada desde el punto, según se explica en la siguiente animación:
DISTANCIA ENTRE PLANOS PARALELOS.
La distancia entre dos planos paralelos quedará determinada por el segmento perpendicular a ambos.
Para calcular la longitud de este segmento tenemos que trazar una recta
perpendicular a los dos planos paralelos y determinar los puntos
intersección en cada uno de ellos, según se puede ver en la siguiente
animación:
 Determinar la distancia entre planos paralelos o entre un punto y un
plano, nos permite resolver las proyecciones diédricas de pirámides,
conos, prismas, cilindros y poliedros.
Determinar la distancia entre planos paralelos o entre un punto y un
plano, nos permite resolver las proyecciones diédricas de pirámides,
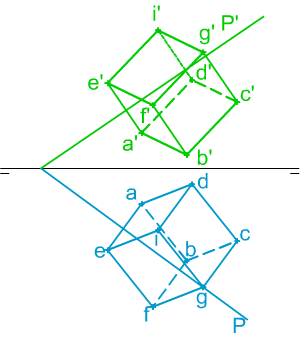
conos, prismas, cilindros y poliedros.En la imagen izquierda tienes las proyecciones diédricas de cubo o hexaedro apoyado en un plano oblicuo, la dificultad de este ejercicio consiste en determinar tanto las proyecciones de la verdadera magnitud de aristas y caras, dada la magnitud del lado, como la del calcular dicha magnitud a partir de las proyecciones diédricas.
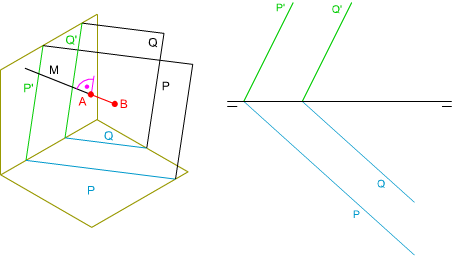 En la imagen izquierda tienes las proyecciones diédricas y la
perspectiva isométrica de los planos paralelos P y Q, tienes que determinar la mínima distancia entre ambos planos.
En la imagen izquierda tienes las proyecciones diédricas y la
perspectiva isométrica de los planos paralelos P y Q, tienes que determinar la mínima distancia entre ambos planos.