3. Con nombre y apellido: Distribución Normal
 |
| Imagen de Arenamontanus bajo licencia Creative Commons |
Ahora sí, vamos ya de lleno con la Distribución Normal.
Acabamos de decir que para calcular probabilidades en una variable continua tenemos que conocer la función de densidad de ésta. Pues bien, si una variable aleatoria continua sigue una distribución normal, debemos conocer antes de nada cuáles son la media μ y la desviación típica σ. Estos dos valores son los parámetros que caracterizan y distinguen cada distribución normal (al igual que "n" y "p" en la binomial.)
Conocidos estos dos parámetros, si X sigue una distribución normal de parámetros μ y σ, X~N(μ , σ), la función de densidad de X será:
Y la representación gráfica, aplicando todo lo que vimos en el tema de representación de funciones (dominio, cortes con ejes, extremos relativos,...) será similar a esta:
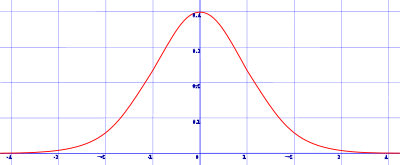
¿Te has recuperado ya del susto? Bueno, no te preocupes que tampoco es que tengamos que utilizar ese pedazo de función para lo que nos interesa.
Ahora ya podríamos calcular la probabilidad de cualquier intervalo en cualquier distribución normal calculando el área que hay bajo esa función de densidad dentro del intervalo en cuestión. Pero eso no es que sea un juego de niños precisamente.
En Matemáticas, esto se hace usando el concepto de integral, algo similar a la operación contraria de la derivada, pero para esta función es tan sumamente complicado que se utilizan otras herramientas para calcular estas probabilidades, aunque en el fondo de esos cálculos están las integrales.
En la siguiente escena, aparece representada la función de densidad de una distribución normal. En los controles "media" y "desv. tip" puedes introducir el valor que quieras de los dos parámetros de la distribución normal y colocando el control "Comenzar" en 1, puedes ver sombreada una parte de esa distribución y dos puntos P y Q que puedes mover libremente. Además, en la esquina superior izquierda, aparece el valor del área de la región sombreada.
Applet Descartes de Ricardo Gutiérrez Ibáñez bajo licencia Creative Commons
Manipula la escena de arriba y contesta a las siguientes cuestiones
- ¿Qué efecto produce sobre la función de densidad aumentar la media? ¿Y disminuirla?
- ¿Qué efecto produce sobre la función de densidad aumentar la desviación típica de la Normal? ¿Y disminuirla?
- Si X es N(0,1), ¿Cuál es la probabilidad de que X esté entre 2,1 y 3,5?
- Si X ~ N(0,1), calcula P(-3<X<0)
- Si X ~ N(0,1), calcula P(X ≥ -1) (Usa el zoom y aleja el punto Q)
- Si X ~ N(1,5 ; 0,6), calcula P(-2<X<2)
- Si X ~ N(-0,5 ; 1,5), calcula P(-2<X<2)
- Si X ~ N(8 , 2), calcula P(0≤X≤10) (Usa el zoom para ver la función)
- Si X ~ N(8 , 2), calcula P(X≥0)
- Si X ~ N(3 ; 0,5), calcula P(X<3)
- Si X ~ N(-2; 0,6), calcula P(X<-2)
 |
| Imagen de kevindooley bajo licencia Creative Commons |
Si te fijas bien en la gráfica de esta función, puedes ver que:
El dominio es el conjunto de todos los números reales.
Respecto a la media, la función es simétrica.
Tiene asíntota horizontal y = 0, tanto cuando x se va a -∞ como a +∞.
La función es creciente hasta que x llega al valor de la media y decreciente a partir de él. Por tanto, en x = μ la función alcanza su máximo.
Otra propiedad curiosa que cumple esta distribución es que las tres medidas de centralización coinciden, es decir, moda, mediana y media coinciden en el valor de μ.