2.2. LLegamos al punto de inflexión
 |
Un punto de inflexión es aquel en el que la función cambia de curvatura, es decir, en el que pasa de cóncava a convexa o viceversa.
Si trazamos una tangente a la función en ese punto se puede apreciar que a un lado del punto la función queda por encima de la recta tangente y al otro lado por debajo.
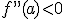 ) a convexa (
) a convexa (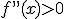 ), lo normal es que en ese punto la función se anule. Compruebalo en la siguiente ventana observando que pasa en los puntos x=-3, x=0 y x=2, que son puntos de inflexión de la función.
), lo normal es que en ese punto la función se anule. Compruebalo en la siguiente ventana observando que pasa en los puntos x=-3, x=0 y x=2, que son puntos de inflexión de la función.
Si no ves correctamente la escena, pulsa aquí
Si una función f cumple en un valor x=a que 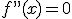 y
y 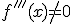 entonces la función tiene en el punto de valor x=a un punto de inflexión.
entonces la función tiene en el punto de valor x=a un punto de inflexión.
Si es complicado el cálculo de la derivada tercera, lo usual es estudiar el signo de la segunda derivada antes y después del punto x=a. Si cambia su signo entonces es punto de inflexión.
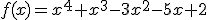
 |
| Foto tomada del Banco de Imágenes del ITR. |
Después del estudio realizado han aproximado la entrega de combustible a la función siguiente:
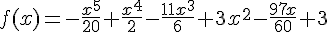
Los puntos de inflexión de esa función se obtienen en:
(1, )
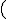 ,
,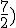
( , )
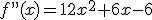 , que se anulaba en los puntos
, que se anulaba en los puntos 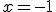 y
y 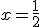 y los intervalos de signo son:
y los intervalos de signo son:
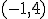 y
y 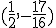 .
.
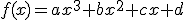 . Basta que impongamos las condiciones que sabemos.
. Basta que impongamos las condiciones que sabemos.
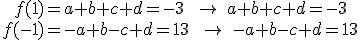
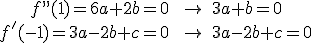
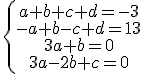 Resolviendo el sistema obtenemos los coeficientes
Resolviendo el sistema obtenemos los coeficientes 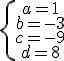 .
.
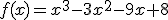 .
.