2. Buscando a quién parecerse.
 |
| 11. Imagen de LatinSud bajo licencia Creative Commons |
En nuestra vida estamos continuamente buscando parecidos. Parecidos físicos entre personas que conocemos y personajes famosos, parecidos entre artículos de nuestra cesta de la compra de los llamados de marca "blanca" y los de marca original, parecidos entre la ropa que me compro y la que anuncian en la publicidad, y podríamos seguir hasta que nos cansáramos.
Pues en matemáticas, también cabe el parecido. Pese al halo de ciencia exacta, en las matemáticas caben las aproximaciones y la búsqueda de modelos a los que ajustar diversas situaciones de la realidad, pero por supuesto, sabiendo controlar cuál es el grado de "parecido". En este tema hemos visto ya varios ejemplos de variables cuyos datos se han obtenido de manera experimental y el objetivo ahora será encontrar una función (el modelo) a la que se puedan ajustar esos datos. Seguramente, no será posible encontrarla de manera exacta, así que, habrá que buscar la que más se parezca.
En el punto 1 del tema hemos estado hablando continuamente de correlación lineal, de si los datos o las variables podrían ajustarse a función lineal (o mejor dicho, a una función cuya gráfica sea una recta.)
Pues bien, ha llegado el momento de buscar esa recta. Esa recta a la que se van ajustar los datos se va a llamar recta de regresión y será la función que haga de modelo al que se parecerá nuestra variable bidimensional. Es decir, diremos que nuestras dos variables se comportan de forma parecida a las variables de la función que da la recta de regresión.
La forma más sencilla de obtener una recta de ajuste es dibujando una recta encima de la nube de puntos, tratando de que dicha recta se ajuste lo mejor posible a la nube de puntos.
En la siguiente escena puedes manipular libremente los puntos rojos, observa lo que ocurre con la recta y con el coeficiente de correlación:
- Acerca los puntos de a la recta. ¿Qué ocurre con r?
- Aléjalos ahora. ¿Qué ocurre?
- Coloca ahora los puntos para que sea decreciente la recta y repite los dos apartados anteriores. ¿Qué valores toma r?
Applet Descartes de Celia Berrocal Sánchez bajo licencia Creative Commons
La recta a la que mejor se ajustan los datos se llama recta de regresión de Y sobre X, y cumple que mientras más próximos estén los datos a esa recta, mayor es el coeficiente de correlación y por tanto, mayor es la relación entre las variables.
Además, la ecuación de dicha recta (recta de regresión de Y sobre X)viene dada por la fórmula:
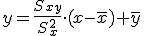
Como comprenderás, esta recta no se elige al azar ni se dibuja donde buenamente se cree. Existe detrás de ella todo un entramado matemático que permite al final sacar la fórmula que ves arriba.
Para empezar hay que elegir un criterio de buena aproximación, y el criterio por el que se elige es el de mínimos cuadrados entre los valores reales de la variable Y, y los valores aproximados, es decir, la recta de regresión es la que hace que la suma de las distancias verticales al cuadrado de los puntos a la recta sea la mínima posible.
En la siguiente escena puedes comprender mejor el método de los mínimos cuadrados.
Aparecen doce puntos que puedes mover libremente con el ratón y dos puntos, que determinan una recta verde, que también se pueden mover libremente por toda la escena. La recta representada en azul es la recta de regresión de Y sobre X. El valor de "d" en color azul es la suma de los cuadrados de las longitudes de los segmentos de color morado, es decir, de las distancias verticales de cada punto a la recta azul.
El valor de "dr" en verde, es el mismo cálculo para la recta verde. Si mueves los puntos o la recta verde, verás que en todo momento la suma de los cuadrados de las distancias a la recta de regresión es menor que a la recta verde, por lo que la recta de regresión es la que hace que el error que se comete al tomar una recta como aproximación de modelo de comportamiento de los puntos sea mínimo.
Applet Descartes de Luis Barrios Calmaestra bajo licencia Creative Commons.
Pero igual que tomamos como criterio que sea mínima la suma de las distancias verticales al cuadrado, podríamos haber tomado como criterio que fuera mínima la suma de las distancias horizontales al cuadrado.
Pues bien, si hacemos eso, obtendremos otra recta de regresión, la de X sobre Y.
 |
Siempre hay dos rectas de regresión, la de Y sobre X y la X sobre Y. Las fórmulas son las que siguen, aunque como puedes ver, para calcular la de X sobre Y, basta con cambiar los papeles de X e Y en la fórmula vista anteriormente.
|
Recta de Regresión de Y sobre X
|
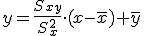 |
|
Recta de Regresión de X sobreY
|
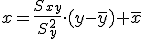 |
Según lo que nos interese, calcularemos una u otra.
En la siguiente escena puedes plantear gráficamente distintos diagramas de dispersión. Aparecen doce puntos que puedes mover libremente por toda la escena con el ratón y en cada momento aparece el coeficiente de correlación de esa distribución. En color verde se representa la recta de regresión de Y sobre X y en color morado, la recta de regresión de X sobre Y.
Puedes ver que las dos rectas siempre se cortan en el punto marcado en azul. Ese punto se llama centro de gravedad de la distribución y sus coordenadas son las dos medias:
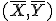
Mueve los puntos y observa lo que ocurre con las rectas.
Applet Descartes de Luis Barrios Calmaestra bajo licencia Creative Commons.
Contesta a las siguientes cuestiones manipulando los puntos de la escena anterior.
- Mueve los puntos hasta conseguir que la correlación sea muy fuerte. ¿Qué ocurre con las rectas?
- Intenta ahora que r se acerque a cero, es decir, que no haya correlación. ¿Qué ocurre con las rectas?
- Si la correlación es positiva, ¿la recta crece o decrece?
- Si la correlación es negativa, ¿la recta crece o decrece?
- Si una recta crece, ¿la otra lo hace también?
 |
| 12. Imagen en Wikimedia Commons bajo licencia Creative Commons |
Karl Pearson (1857-1936), matemático y filósofo de las ciencias británico, se le conoce por haber desarrollado algunas de las técnicas centrales de la moderna estadística, y por aplicar estas técnicas a los problemas de la herencia biológica.
A principios de 1900, Pearson se interesó por el trabajo de Francis Galton, que intentaba encontrar relaciones estadísticas para explicar cómo las características biológicas iban pasando a través de sucesivas generaciones. La investigación de Pearson colocó en gran medida las bases de la estadística del siglo XX, definiendo los significados de correlación, análisis de la regresión y desviación típica. En 1911 Pearson alcanzó el cargo de profesor de eugenesia en el University College, examinando la recopilación y análisis de la información en el sentido que las características como inteligencia, criminalidad, pobreza y creatividad se transmiten a través de generaciones. Pearson confiaba en aplicar estas intuiciones con el fin de mejorar la raza humana.
Si quieres saber más sobre el trabajo de K. Pearson, sigue el enlace.