1.1. Muy agudo, sí señor
Seguimos con el alquiler de la grúa para pintar la fachada.
En la siguiente escena puedes manipular tanto el ángulo del brazo como la longitud. El punto naranja representa la base de la grúa, y el rojo la plataforma. Si marcas la casilla del rótulo "Muestra altura", aparecerá representada la altura que alcanza la plataforma.
No cabe duda de que a más ángulo y mayor longitud del brazo, más altura alcanzará la plataforma. La cuestión es cómo averiguar la altura conociendo el ángulo y la longitud del brazo. Aquí es donde entra en acción la trigonometría.
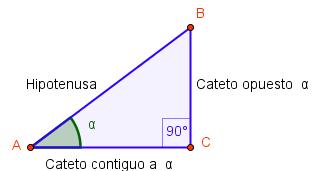
En esta otra escena aparece representado un triángulo rectángulo ABC. Puedes modificar la amplitud de uno de los ángulos no rectos (mueve el ángulo α), y la del cateto contiguo a él (para ello, mueve el punto C).
¿Habrá alguna relación entre la longitud de α, y la de los lados del triángulo rectángulo? Si así fuera, ya podríamos calcular la altura de la plataforma de la grúa.
Escribe todas las longitudes con los decimales que indica la escena.
|
Longitud del cateto
contiguo a α, |
Longitud de la
hipotenusa |
Longitud del cateto
opuesto a α, |
Cociente entre el cateto opuesto
y la hipotenusa |
| 12 | 13,856 |
6,928 |
|
| 14 | 16,166 |
|
|
| 20 |
|
11,547 |
|
| 28 |
|
0,5 |
Podemos afirmar que fijado el ángulo α en 30º, para cualquier triángulo rectángulo que construyamos sobre él, la relación que existe entre el cateto y la es igual a .
a) Ahora fija como ángulo α = 40º. Haz una tabla similar a la anterior. ¿Cuál sería ahora ese valor constante entre el cociente del cateto opuesto a 40º y la hipotenusa?
b) ¿Y si tomáramos α = 55º?
Los tres ángulos con los que hemos trabajado en las autoevaluaciones anteriores, 30º, 40º y 55º, son menores que el ángulo recto. Es decir, son ángulos agudos, pues está comprendidos entre 0º y 90º.
A continuación definiremos las razones trigonométricas de un ángulo agudo, es decir, el seno, coseno y tangente.
Para un ángulo agudo α se define el seno de α, se escribe sen α, como el cociente entre el cateto opuesto a α y la hipotenusa del triángulo rectángulo ABC construido sobre α.
 |
sen α = 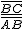
Como hemos podido comprobar, el valor del seno de α no depende del tamaño del triángulo ABC.
Muchas de las matemáticas de la antigüedad entraron en Europa a traves de las traducciones que se hacían del árabe al latín en las bibliotecas de la ciudad española de Toledo, durante los siglos XI y XII.
Y es precisamente el traductor inglés Roberto de Chester, que trabajó en España hacia la mitad del siglo XII, quién utiliza por primera vez la expresión "sinus" para referirse al seno de un ángulo.
En las matemáticas hindú se utilizó el término "jiva" para designar al seno, posteriormente los árabes lo transforman en "jiba". Pero en árabe también existe la palabra "jaib", cuyo significado es bahía o ensenada.
Y es ahí cuando Roberto de Chester confunde ambas palabras, y traduce "jiva" por "sinus", que en latín significa precisamente bahía.
 |
Hasta las décadas de los 70 y 80 del siglo pasado, si una persona quería hallar el seno u otra razón trigonométrica de un ángulo, debía utilizar las tablas trigonométricas. Como su propio nombre indica, eran un larga y abigarrada lista que comprendía ángulos desde 0º a 45º, con su correspondiente seno.
Si el ángulo del que se quería saber el seno estaba incluido en la lista, la respuesta era rápida. Pero, si eso no era así, empezaba un calvario de operaciones y fórmulas hasta llegar al valor buscado.
Gracias a la aparición y popularización de las calculadoras científicas, en la actualidad, para hallar la razón trigonométrica de un ángulo sólo tenemos que pulsar dos o tres teclas, y en décimas de segundos, tenemos la respuesta deseada.
Por ejemplo, para calcular el seno del ángulo de 32º, basta con pulsar la tecla ![]() y después 32. En el siguiente apartado veremos esto con más detenimiento.
y después 32. En el siguiente apartado veremos esto con más detenimiento.
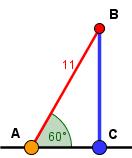 |
Hagamos memoria. La fachada de mi casa medía 8 metros de largo y 10 de alto. La plataforma más económica se podía abrir hasta un máximo de 60º y el brazo alcanzaba un máximo de 11 metros.
¿Puedo pintar la fachada con esa grúa? ¿Alcanza hasta los 10 metros?
Con un proceso muy similar al del seno se construye el coseno y la tangente de un ángulo agudo. Veamos con más detalle, en las siguientes animaciones del ITE del Ministerio de Educación, los pasos que hay que dar.
|
|
|
| En el caso del coseno, una vez construido el triángulo rectángulo sobre el ángulo, realizamos el cociente entre el cateto contiguo y la hipotensua. |
Para la tangente, el cociente que se realiza es entre el cateto opuesto y el cateto contiguo |
Al igual que ocurría con el seno, el coseno y la tangente de un ángulo no dependen del tamaño del triángulo rectángulo que se construya sobre él.
 |
Para un ángulo agudo α se define el coseno de α, se escribe cos α, como el cociente entre el cateto contiguo a α y la hipotenusa del triángulo rectángulo ABC construido sobre α.
cos α = 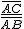
De manera similar, se define la tangente de α, se escribe tg α, como el cociente entre el cateto opuesto a α y el cateto contiguo del triángulo rectángulo ABC construido sobre α.
tg α =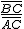
Para repasar los conceptos que se han definido en este apartado, puedes trabajar con el siguiente enlace:
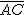
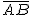
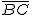
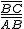
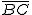 para un ángulo α de 60º y una longitud del brazo de 11 metros.
para un ángulo α de 60º y una longitud del brazo de 11 metros.
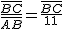 , luego despejando
, luego despejando 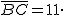 sen 60º = 11· 0,866 = 9,52
sen 60º = 11· 0,866 = 9,52