2.1. Tetraedro
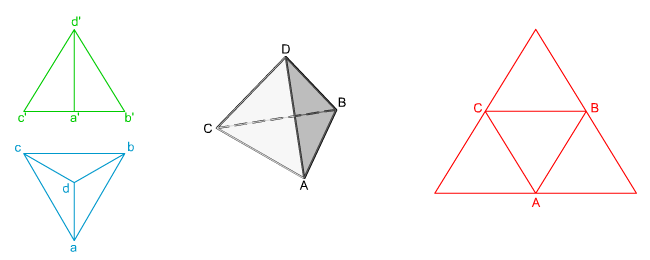
Su estudio nos ayudará a comprender las características de las pirámides regulares.
En la imagen superior puedes ver su representación diédrica, la perspectiva y su desarrollo.
Sección principal.
Para determinar la altura de un tetraedro debemos realizar la sección principal, esta viene determinada por un plano que pasa por una arista del poliedro, por su centro geométrico, y perpendicularmente por el punto medio de la arista opuesta.
En la siguiente animación puedes ver cómo mediante la sección principal de un tetraedro obtenemos un triángulo isósceles, lo que nos permite determinar la altura del poliedro.
Determinar la altura de un tetraedro.
Existe otro método, basado en la sección principal, para determinar la altura de un tetraedro: el abatimiento del triángulo rectángulo formado por una arista, su proyección y dicha altura.
En la animación inferior te mostramos el procedimiento seguir, compáralo con el método anterior y verás que es más directo y sencillo.
En el siguiente vídeo puedes ver cómo se obtienen las proyecciones diédricas de un tetraedro apoyado en el plano de proyección horizontal (PHP).
Posiciones de un Tetraedro.
Un tetraedro puede ocupar infinitas posiciones respecto de los planos de proyección, nosotros vamos a resumirlas en las tres más usuales respecto del PHP, apoyado en dicho plano por una de sus caras, por una de sus aristas y por un vértice.
En la animación inferior te mostramos estas tres disposiciones.
Tetraedo apoyado en el PHP por una de sus aristas, siendo la opuesta una recta horizontal.
La proyección horizontal de esta peculiar posición es un cuadrado y sus diagonales, que son las aristas en verdadera magnitud.Para representar la proyección vertical tenemos que determinar la distancia entre las aristas opuestas mediante el triángulo rectángulo definido por la mediana de una de las caras, la mitad de su proyección y la distancia anteriormente mencionada.
En la siguiente animación puedes ver el procedimiento a seguir en su representación diédrica.
Tetraedro apoyado en un plano oblicuo.
Cuando un tetraedro tiene una de sus caras apoyada en un plano cualquiera primero debemos determinar sus proyecciones, mediante el abatimiento, luego determinar su altura, y finalmente, colocar dicha altura sobre una recta que pase por el centro geométrico de dicha cara, perpendicular al plano dado.
En la animación inferior te mostramos de manera detallada el procedimiento a seguir.
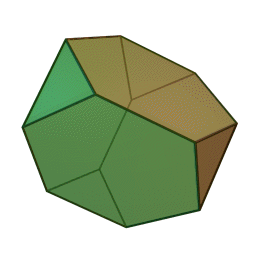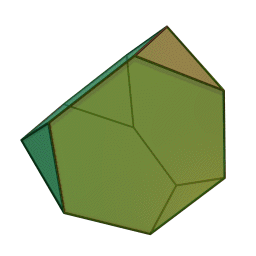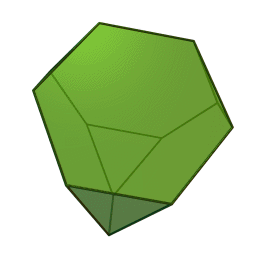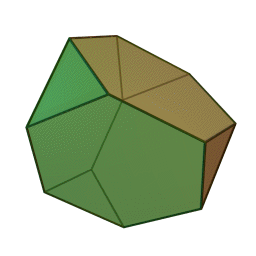 |
El Tetraedro truncado es el menor de los sólidos de Arquímedes, se obtiene truncando cada vértice de un tetraedro de manera que se obtienen 8 caras: 4 del tetraedro original que se convierten de triangulares a hexagonales y 4 nuevas que resultan de los vértices, en este caso triangulares. |
|
|
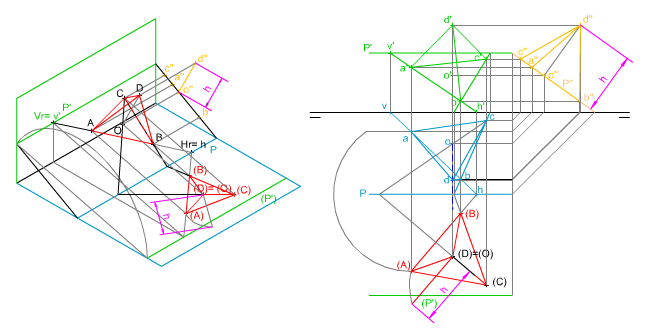
| En la imagen superior puedes ver cómo se han determinado las proyecciones diédricas de un tetraedro apoyado por su cara ABCD en un plano paralelo a la LT.
Conocemos la proyección horizontal de una de sus aristas así como las trazas el plano P. Te pedimos que apliques los contenidos y procedimientos adquiridos hasta ahora para determinar sus proyecciones diédricas mediante las herramientas de dibujo tradicionales. |